北京市2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 如图是某几何体的三视图,该几何体是( )
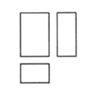 A、圆柱 B、圆锥 C、三棱锥 D、长方体2. 2020年6月23日,北斗三号最后一颗全球组网卫星从西昌发射中心发射升空,6月30日成功定点于距离地球36000公里的地球同步轨道.将36000用科学记数法表示应为( )A、 B、 C、 D、3. 如图,AB和CD相交于点O,则下列结论正确的是( )
A、圆柱 B、圆锥 C、三棱锥 D、长方体2. 2020年6月23日,北斗三号最后一颗全球组网卫星从西昌发射中心发射升空,6月30日成功定点于距离地球36000公里的地球同步轨道.将36000用科学记数法表示应为( )A、 B、 C、 D、3. 如图,AB和CD相交于点O,则下列结论正确的是( )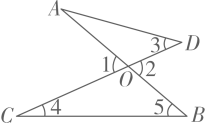 A、∠1=∠2 B、∠2=∠3 C、∠1>∠4+∠5 D、∠2<∠54. 下列图形中,既是中心对称图形也是轴对称图形的是( )A、
A、∠1=∠2 B、∠2=∠3 C、∠1>∠4+∠5 D、∠2<∠54. 下列图形中,既是中心对称图形也是轴对称图形的是( )A、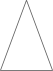 B、
B、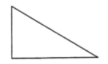 C、
C、 D、
D、 5. 正五边形的外角和为( )A、180° B、360° C、540° D、720°6. 实数a在数轴上的对应点的位置如图所示.若实数 满足 ,则b的值可以是( )
5. 正五边形的外角和为( )A、180° B、360° C、540° D、720°6. 实数a在数轴上的对应点的位置如图所示.若实数 满足 ,则b的值可以是( )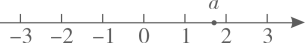 A、2 B、-1 C、-2 D、-37. 不透明的袋子中装有两个小球,上面分别写着“1”,“2”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )A、 B、 C、 D、8. 有一个装有水的容器,如图所示.容器内的水面高度是10cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( )
A、2 B、-1 C、-2 D、-37. 不透明的袋子中装有两个小球,上面分别写着“1”,“2”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )A、 B、 C、 D、8. 有一个装有水的容器,如图所示.容器内的水面高度是10cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( )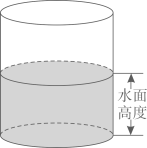 A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系
A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系二、填空题
-
9. 若代数式 有意义,则实数x的取值范围是 .10. 已知关于 的方程 有两个相等的实数根,则k的值是 .11. 写出一个比 大且比 小的整数 .12. 方程组 的解为 .13. 在平面直角坐标系 中,直线 与双曲线 交于A,B两点.若点A,B的纵坐标分别为 ,则 的值为 .14. 在 ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明 ABD≌ ACD,这个条件可以是(写出一个即可)
 15. 如图所示的网格是正方形网格,A,B,C,D是网格交点,则 ABC的面积与 ABD的面积的大小关系为: (填“>”,“=”或“<”)
15. 如图所示的网格是正方形网格,A,B,C,D是网格交点,则 ABC的面积与 ABD的面积的大小关系为: (填“>”,“=”或“<”)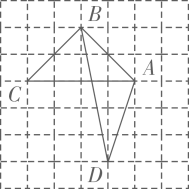 16. 如图是某剧场第一排座位分布图:甲、乙、丙、丁四人购票,所购票分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序 .
16. 如图是某剧场第一排座位分布图:甲、乙、丙、丁四人购票,所购票分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序 .
三、解答题
-
17. 计算:18. 解不等式组:19. 已知 ,求代数式 的值.20. 已知:如图, ABC为锐角三角形,AB=BC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP= .
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作线段.
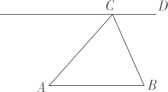 (1)、使用直尺和圆规,依作法补全图形(保留作图痕迹)(2)、完成下面的证明.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹)(2)、完成下面的证明.证明:∵CD∥AB,
∴∠ABP= .
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC= ∠BAC()(填推理依据)
∴∠ABP= ∠BAC
21. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF. (1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.22. 在平面直角坐标系 中,一次函数 的图象由函数 的图象平移得到,且经过点(1,2).(1)、求这个一次函数的解析式;(2)、当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.23. 如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.
(1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.22. 在平面直角坐标系 中,一次函数 的图象由函数 的图象平移得到,且经过点(1,2).(1)、求这个一次函数的解析式;(2)、当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.23. 如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.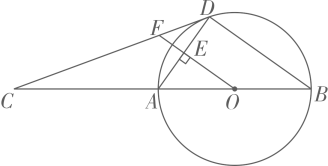 (1)、求证:∠ADC=∠AOF;(2)、若sinC= ,BD=8,求EF的长.24. 小云在学习过程中遇到一个函数 .下面是小云对其探究的过程,请补充完整:(1)、当 时,对于函数 ,即 ,当 时, 随x的增大而 , 且 ;对于函数 ,当 时, 随x的增大而 , 且 ;结合上述分析,进一步探究发现,对于函数 ,当 时,y随x的增大而 .(2)、当 时,对于函数 ,当 时,y与x的几组对应值如下表:
(1)、求证:∠ADC=∠AOF;(2)、若sinC= ,BD=8,求EF的长.24. 小云在学习过程中遇到一个函数 .下面是小云对其探究的过程,请补充完整:(1)、当 时,对于函数 ,即 ,当 时, 随x的增大而 , 且 ;对于函数 ,当 时, 随x的增大而 , 且 ;结合上述分析,进一步探究发现,对于函数 ,当 时,y随x的增大而 .(2)、当 时,对于函数 ,当 时,y与x的几组对应值如下表:x
0
1
2
3
y
0
1
综合上表,进一步探究发现,当 时,y随x的增大而增大.在平面直角坐标系 中,画出当 时的函数y的图象.
 (3)、过点(0,m)( )作平行于x轴的直线l,结合(1)(2)的分析,解决问题:若直线l与函数 的图象有两个交点,则m的最大值是 .25. 小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
(3)、过点(0,m)( )作平行于x轴的直线l,结合(1)(2)的分析,解决问题:若直线l与函数 的图象有两个交点,则m的最大值是 .25. 小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:a.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
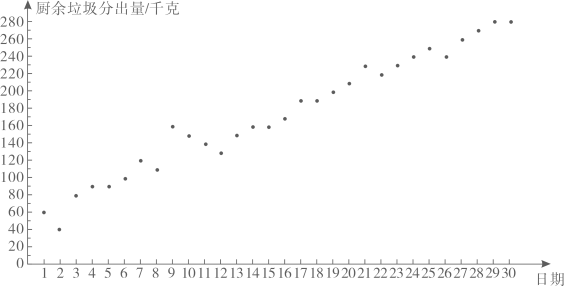
b.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段
1日至10日
11日至20日
21日至30日
平均数
100
170
250
(1)、该小区5月1日至30日的厨余垃圾分出量的平均数约为(结果取整数)(2)、已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的倍(结果保留小数点后一位);(3)、记该小区5月1日至10日的厨余垃圾分出量的方差为 5月11日至20日的厨余垃圾分出量的方差为 ,5月21日至30日的厨余垃圾分出量的方差为 .直接写出 的大小关系.26. 在平面直角坐标系 中, 为抛物线 上任意两点,其中 .(1)、若抛物线的对称轴为 ,当 为何值时,(2)、设抛物线的对称轴为 .若对于 ,都有 ,求t的取值范围.27. 在 中,∠C=90°,AC>BC,D是AB的中点.E为直线上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF.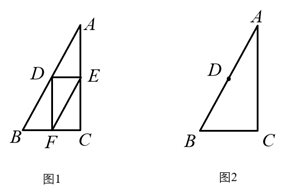 (1)、如图1,当E是线段AC的中点时,设 ,求EF的长(用含 的式子表示);(2)、当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE,EF,BF之间的数量关系,并证明.28. 在平面直角坐标系 中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦 ( 分别为点A,B的对应点),线段 长度的最小值称为线段AB到⊙O的“平移距离”.
(1)、如图1,当E是线段AC的中点时,设 ,求EF的长(用含 的式子表示);(2)、当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE,EF,BF之间的数量关系,并证明.28. 在平面直角坐标系 中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦 ( 分别为点A,B的对应点),线段 长度的最小值称为线段AB到⊙O的“平移距离”.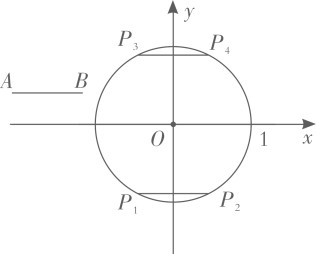 (1)、如图,平移线段AB到⊙O的长度为1的弦 和 ,则这两条弦的位置关系是;在点 中,连接点A与点的线段的长度等于线段AB到⊙O的“平移距离”;(2)、若点A,B都在直线 上,记线段AB到⊙O的“平移距离”为 ,求 的最小值;(3)、若点A的坐标为 ,记线段AB到⊙O的“平移距离”为 ,直接写出 的取值范围.
(1)、如图,平移线段AB到⊙O的长度为1的弦 和 ,则这两条弦的位置关系是;在点 中,连接点A与点的线段的长度等于线段AB到⊙O的“平移距离”;(2)、若点A,B都在直线 上,记线段AB到⊙O的“平移距离”为 ,求 的最小值;(3)、若点A的坐标为 ,记线段AB到⊙O的“平移距离”为 ,直接写出 的取值范围.