安徽省2020年中考数学试卷
试卷更新日期:2020-07-28 类型:中考真卷
一、单选题
-
1. 下列各数中比-2小的数是( )A、-3 B、-1 C、0 D、22. 计算 的结果是( )A、 B、 C、 D、3. 下列四个几何体中,主视图为三角形的是( )A、
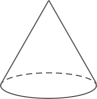 B、
B、 C、
C、 D、
D、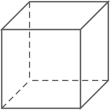 4. 安徽省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示为( )A、0.547 B、 C、 D、5. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、6. 冉冉的妈妈在网上销售装饰品.最近一周, 每天销售某种装饰品的个数为:.11,10,11,13,11,13,15关于这组数据,冉冉得出如下结果,其中错误的是( )A、众数是11 B、平均数是12 C、方差是 D、中位数是137. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、8. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
4. 安徽省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示为( )A、0.547 B、 C、 D、5. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、6. 冉冉的妈妈在网上销售装饰品.最近一周, 每天销售某种装饰品的个数为:.11,10,11,13,11,13,15关于这组数据,冉冉得出如下结果,其中错误的是( )A、众数是11 B、平均数是12 C、方差是 D、中位数是137. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、8. 如图, 中, ,点D在 上, .若 ,则 的长度为( )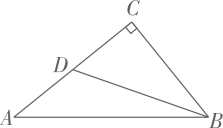 A、 B、 C、 D、49. 已知点 在 上.则下列命题为真命题的是( )A、若半径 平分弦 .则四边形 是平行四边形 B、若四边形 是平行四边形.则 C、若 .则弦 平分半径 D、若弦 平分半径 .则半径 平分弦10. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、 B、 C、 D、49. 已知点 在 上.则下列命题为真命题的是( )A、若半径 平分弦 .则四边形 是平行四边形 B、若四边形 是平行四边形.则 C、若 .则弦 平分半径 D、若弦 平分半径 .则半径 平分弦10. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )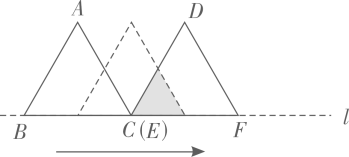 A、
A、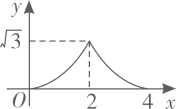 B、
B、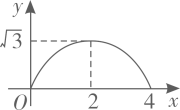 C、
C、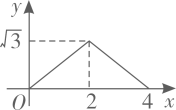 D、
D、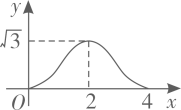
二、填空题
-
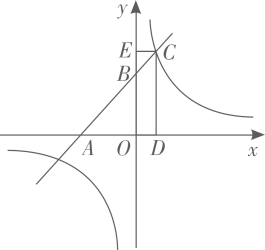
11. 计算: =.12. 分解因式: = .13. 如图,一次函数 的图象与x轴和y轴分别交于点A和点B与反比例函数 上的图象在第一象限内交于点 轴, 轴,垂足分别为点 ,当矩形 与 的面积相等时,k的值为 .
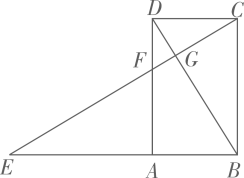
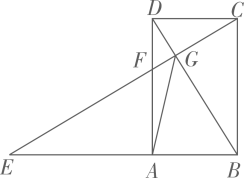
 14. 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片 沿过点A的直线折叠,使得点B落在 上的点 处,折痕为 ;再将 分别沿 折叠,此时点 落在 上的同一点R处.请完成下列探究:
14. 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片 沿过点A的直线折叠,使得点B落在 上的点 处,折痕为 ;再将 分别沿 折叠,此时点 落在 上的同一点R处.请完成下列探究: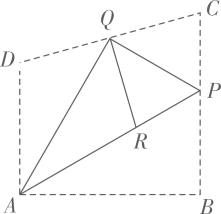 (1)、 的大小为 ;(2)、当四边形 是平行四边形时 的值为 .
(1)、 的大小为 ;(2)、当四边形 是平行四边形时 的值为 .三、解答题
-
15. 解不等式:16. 如图1,在由边长为 个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为端点的线段 ,线段 在网格线上,
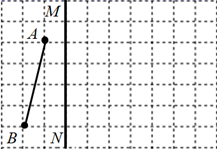 (1)、画出线段 关于线段 所在直线对称的线段 (点 分别为 的对应点);(2)、将线段 ,绕点 ,顺时针旋转 得到线段 ,画出线段 .17. 观察以下等式:
(1)、画出线段 关于线段 所在直线对称的线段 (点 分别为 的对应点);(2)、将线段 ,绕点 ,顺时针旋转 得到线段 ,画出线段 .17. 观察以下等式:第1个等式:
第 个等式:
第3个等式:
第 个等式:
第5个等式:
······
按照以上规律.解决下列问题:
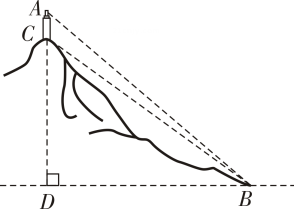
(1)、写出第6个等式;(2)、写出你猜想的第n个等式:(用含n的等式表示),并证明.18. 如图,山顶上有一个信号塔 ,已知信号塔高 米,在山脚下点B处测得塔底C的仰角 ,塔顶A的仰角 .求山高 (点 在同一条竖直线上).(参考数据: )
 19. 某超市有线上和线下两种销售方式.与2019年4月份相比.该超市2020年4月份销售总额增长 其中线上销售额增长 .线下销售额增长 ,(1)、设2019年4月份的销售总额为 元.线上销售额为x元,请用含 的代数式表示2020年4月份的线下销售额(直接在表格中填写结果);
19. 某超市有线上和线下两种销售方式.与2019年4月份相比.该超市2020年4月份销售总额增长 其中线上销售额增长 .线下销售额增长 ,(1)、设2019年4月份的销售总额为 元.线上销售额为x元,请用含 的代数式表示2020年4月份的线下销售额(直接在表格中填写结果);时间 销售总额(元) 线上销售额(元) 线下销售额 2019年4月份 a x a-x 2020年4月份 1.1a 1.43x (2)、求2020年4月份线上销售额与当月销售总额的比值.20. 如图, 是半圆O的直径, 是半圆O上不同于 的两点 与 相交于点 是半圆O所任圆的切线,与 的延长线相交于点E,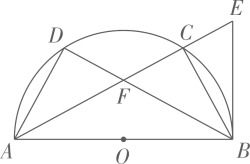 (1)、求证: ;(2)、若 求 平分 .21. 某单位食堂为全体名职工提供了 四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取 名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)、求证: ;(2)、若 求 平分 .21. 某单位食堂为全体名职工提供了 四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取 名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下: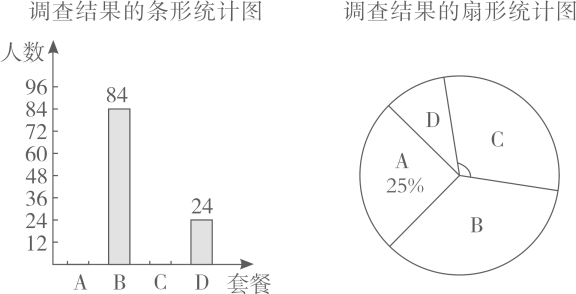 (1)、在抽取的240人中最喜欢A套餐的人数为 ,扇形统计图中“C”对应扇形的圆心角的大小为;(2)、依据本次调查的结果,估计全体960名职工中最喜欢B套餐的人数;
(1)、在抽取的240人中最喜欢A套餐的人数为 ,扇形统计图中“C”对应扇形的圆心角的大小为;(2)、依据本次调查的结果,估计全体960名职工中最喜欢B套餐的人数;