2020年暑期衔接训练青岛版数学八年级下册:第17讲 一次函数与二元一次方程
试卷更新日期:2020-07-28 类型:复习试卷
一、单选题
-
1. 若一次函数y1=k1x+b1与一次函数y2=k2x+b2的图象没有交点,则方程组 的解的情况是( )A、有无数组解 B、有两组解 C、只有一组解 D、没有解2. 用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象如图所示,则所列的二元一次方程组是( )
 A、 B、 C、 D、3. 如图,函数 和 的图象交于点P,则根据图象可得,关于x,y的二元一次方程组 中的解是
A、 B、 C、 D、3. 如图,函数 和 的图象交于点P,则根据图象可得,关于x,y的二元一次方程组 中的解是 A、 B、 C、 D、4. 若方程组 的解为 ,则直线y=mx+n与y=﹣ex+f的交点坐标为( )A、(﹣4,6) B、(4,6) C、(4,﹣6) D、(﹣4,﹣6)5. 已知函数 , , 的图象交于一点,则 值为( ).
A、 B、 C、 D、4. 若方程组 的解为 ,则直线y=mx+n与y=﹣ex+f的交点坐标为( )A、(﹣4,6) B、(4,6) C、(4,﹣6) D、(﹣4,﹣6)5. 已知函数 , , 的图象交于一点,则 值为( ).
A、 B、 C、 D、6. 以一个二元一次方程组中的两个方程作为一次函数画图象,所得的两条直线( )A、有一个交点 B、有无数个交点 C、没有交点 D、以上都有可能7. 在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点.设k为整数,当直线y=x﹣2与y=kx+k的交点为整点时,k的值可以取( )A、4个 B、5个 C、6个 D、7个8. 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论中①k<0;②a>0;③当x<3时,y1<y2;④方程组 的解是 . 正确的个数是( )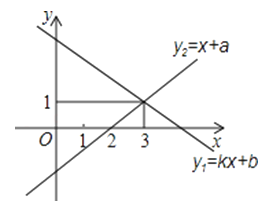 A、1个 B、2个 C、3个 D、4个9. 若直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则整数m的值为( )A、-3,-2,-1,0 B、-2,-1,0,1 C、-1,0,1,2 D、0,1,2,310. 若方程组有无穷多组解,则2k+b2的值为( )A、4 B、5 C、8 D、1011. 某校九年级(2)班40名同学这“希望工程”捐款,共捐款100元,捐款情况如下表:
A、1个 B、2个 C、3个 D、4个9. 若直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则整数m的值为( )A、-3,-2,-1,0 B、-2,-1,0,1 C、-1,0,1,2 D、0,1,2,310. 若方程组有无穷多组解,则2k+b2的值为( )A、4 B、5 C、8 D、1011. 某校九年级(2)班40名同学这“希望工程”捐款,共捐款100元,捐款情况如下表:捐款(元)
1
2
3
4
人数
6

7
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚,若设捐款2元的有x名同学,捐款3元的有y名同学,假设(x,y)是两个一次函数图象的交点,则这两个一次函数解析式分别是( )
A、y=27﹣x与y=x+22 B、y=27﹣x与y=x+ C、y=27﹣x与y=x+33 D、y=27﹣x与y=x+3312. 已知P(x,y)是平面直角坐标系上的一个点,且它的横、纵坐标是一次方程组(a为任意实数)的解,则当a变化时,点P一定不会经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题
-
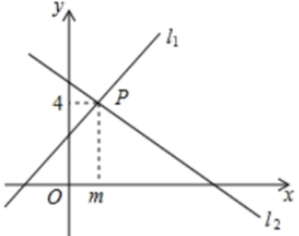
13. 若二元一次方程组 的解是 则一次函数 的图象与一次函数 的图象的交点坐标为 .14. 如图,直线 与直线 相交于点 ,则方程组 的解是.
 15. 如图,已知一次函数y=kx-b与y= x的图像相交于点A(a,1),则关于x的方程 的解x=.
15. 如图,已知一次函数y=kx-b与y= x的图像相交于点A(a,1),则关于x的方程 的解x=. 16. 在平面直角坐标系xOy中,二元一次方程ax+by=c的图象如图所示.则当x=3时,y的值为.
16. 在平面直角坐标系xOy中,二元一次方程ax+by=c的图象如图所示.则当x=3时,y的值为. 17. 若一次函数y=3x+7的图象与y轴的交点坐标满足二元一次方程﹣2x+my=18,则m的值为 .18. 若一次函数y=3x-5的图像l1与y=2x+1的图像l2相交于点P,则点P的坐标是( , )。19. 在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组 的解是.
17. 若一次函数y=3x+7的图象与y轴的交点坐标满足二元一次方程﹣2x+my=18,则m的值为 .18. 若一次函数y=3x-5的图像l1与y=2x+1的图像l2相交于点P,则点P的坐标是( , )。19. 在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组 的解是. 20. 如果 是方程组 的解,则一次函数y=mx+n的解析式为
20. 如果 是方程组 的解,则一次函数y=mx+n的解析式为三、解答题
-
21. 用图象法解方程组 .
 22. 如图,直线y=﹣2x+6与直线y=mx+n相交于点M(p,4).
22. 如图,直线y=﹣2x+6与直线y=mx+n相交于点M(p,4).(1)求p的值;
(2)直接写出关于x,y的二元一次方程组的解;
(3)判断直线y=3nx+m﹣2n是否也过点M?并说明理由.
 23. 在直角坐标系中,直线l1经过点(1,﹣3)和(3,1),直线l2经过(1,0),且与直线l1交于点A(2,a).
23. 在直角坐标系中,直线l1经过点(1,﹣3)和(3,1),直线l2经过(1,0),且与直线l1交于点A(2,a).(1)求a的值;
(2)A(2,a)可看成怎样的二元一次方程组的解?
(3)设直线l1与y轴交于点B,直线l2与y轴交于点C,求△ABC的面积.
24. (1)求一次函y=2x﹣2的图象l1与y=x﹣1的图象l2的交点P的坐标.(2)求直线l1与y轴交点A的坐标;求直线l2与x轴的交点B的坐标;
(3)求由三点P、A、B围成的三角形的面积.
四、综合题
