2020年高考数学真题分类汇编专题11：平面解析几何（综合题）

试卷更新日期：2020-07-27 类型：二轮复习

进入出卷网下载

一、解答题

1. 已知椭圆 $C ： \frac{x^{2}}{25} + \frac{y^{2}}{m^{2}} = 1 (0 < m < 5)$ 的离心率为 $\frac{\sqrt{15}}{4}$ ，A，B分别为C的左、右顶点．

(1)、求C的方程；

(2)、若点P在C上，点Q在直线 $x = 6$ 上，且 $| B P | = | B Q |$ ， $B P ⊥ B Q$ ，求 $△ A P Q$ 的面积．

查看试题解析
2. 已知椭圆C₁： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ (a>b>0)的右焦点F与抛物线C₂的焦点重合，C₁的中心与C₂的顶点重合．过F且与x轴重直的直线交C₁于A，B两点，交C₂于C，D两点，且|CD|= $\frac{4}{3}$ |AB|．

(1)、求C₁的离心率；

(2)、若C₁的四个顶点到C₂的准线距离之和为12，求C₁与C₂的标准方程．

查看试题解析
3. 已知椭圆C₁： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ (a>b>0)的右焦点F与抛物线C₂的焦点重合，C₁的中心与C₂的顶点重合.过F且与x轴垂直的直线交C₁于A，B两点，交C₂于C，D两点，且|CD|= $\frac{4}{3}$ |AB|.

(1)、求C₁的离心率；

(2)、设M是C₁与C₂的公共点，若|MF|=5，求C₁与C₂的标准方程.

查看试题解析
4. 已知A、B分别为椭圆E： $\frac{x^{2}}{a^{2}} + y^{2} = 1$ （a>1）的左、右顶点，G为E的上顶点， $\vec{A G} \cdot \vec{G B} = 8$ ，P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D．

(1)、求E的方程；

(2)、证明：直线CD过定点.

查看试题解析
5. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点M（2，3），点A为其左顶点，且AM的斜率为 $\frac{1}{2}$ ，

(1)、求C的方程；

(2)、点N为椭圆上任意一点，求△AMN的面积的最大值.

查看试题解析
6. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，且过点A（2，1）．

(1)、求C的方程：

(2)、点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

查看试题解析
7. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的一个顶点为 $A (0, - 3)$ ，右焦点为F，且 $| O A | = | O F |$ ，其中O为原点．
（Ⅰ）求椭圆的方程；

（Ⅱ）已知点C满足 $3 \vec{O C} = \vec{O F}$ ，点B在椭圆上（B异于椭圆的顶点），直线 $A B$ 与以C为圆心的圆相切于点P，且P为线段 $A B$ 的中点．求直线 $A B$ 的方程．

查看试题解析
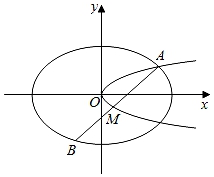
8. 在平面直角坐标系xOy中，已知椭圆 $E ： \frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 的左、右焦点分别为F₁ ， F₂ ，点A在椭圆E上且在第一象限内，AF₂⊥F₁F₂ ，直线AF₁与椭圆E相交于另一点B．

(1)、求△AF₁F₂的周长；

(2)、在x轴上任取一点P，直线AP与椭圆E的右准线相交于点Q，求 $\vec{O P} \cdot \vec{Q P}$ 的最小值；

(3)、设点M在椭圆E上，记△OAB与△MAB的面积分别为S₁ ， S₂ ，若S₂=3S₁ ，求点M的坐标．

查看试题解析
9. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 过点 $A (- 2, - 1)$ ，且 $a = 2 b$ ．
（Ⅰ）求椭圆C的方程：

（Ⅱ）过点 $B (- 4, 0)$ 的直线l交椭圆C于点 $M, N$ ,直线 $M A, N A$ 分别交直线 $x = - 4$ 于点 $P, Q$ ．求 $\frac{| P B |}{| B Q |}$ 的值．

查看试题解析
10. 如图，已知椭圆C₁： $\frac{x^{2}}{2}$ +y²＝1，抛物线C₂：y²＝2px（p＞0），点A是椭圆C₁与抛物线C₂的交点，过点A的直线l交椭圆C₁于点B，交抛物线C₂于M（B，M不同于A）．
（Ⅰ）若p＝ $\frac{1}{16}$ ，求抛物线C₂的焦点坐标；
（Ⅱ）若存在不过原点的直线l使M为线段AB的中点，求p的最大值．

查看试题解析