2020年高考数学真题分类汇编专题09:三角函数
试卷更新日期:2020-07-27 类型:二轮复习
一、单选题
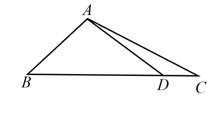
-
1. 已知函数f(x)=sinx+ ,则( )A、f(x)的最小值为2 B、f(x)的图像关于y轴对称 C、f(x)的图像关于直线 对称 D、f(x)的图像关于直线 对称2. 已知 ,则 ( )A、 B、 C、 D、3. 在△ABC中,cosC= ,AC=4,BC=3,则tanB=( )A、 B、2 C、4 D、84. 在△ABC中,cosC= ,AC=4,BC=3,则cosB=( )A、 B、 C、 D、5. 已知2tanθ–tan(θ+ )=7,则tanθ=( )A、–2 B、–1 C、1 D、26. 若α为第四象限角,则( )A、cos2α>0 B、cos2α<0 C、sin2α>0 D、sin2α<07. 已知 ,且 ,则 ( )A、 B、 C、 D、8. 设函数 在 的图像大致如下图,则f(x)的最小正周期为( )
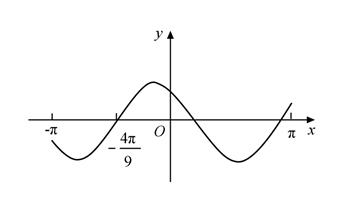 A、 B、 C、 D、9. 已知函数 .给出下列结论:
A、 B、 C、 D、9. 已知函数 .给出下列结论:① 的最小正周期为 ;② 是 的最大值;③把函数 的图象上所有点向左平移 个单位长度,可得到函数 的图象.其中所有正确结论的序号是( )
A、① B、①③ C、②③ D、①②③二、多选题
-
10. 下图是函数y= sin(ωx+φ)的部分图像,则sin(ωx+φ)= ( )
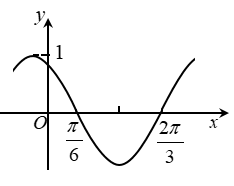
A、 B、 C、 D、三、填空题
-
11. 关于函数f(x)= 有如下四个命题:
①f(x)的图像关于y轴对称.
②f(x)的图像关于原点对称.
③f(x)的图像关于直线x= 对称.
④f(x)的最小值为2.
其中所有真命题的序号是 .
12. 若 ,则 .13. 如图,在三棱锥P–ABC的平面展开图中,AC=1, ,AB⊥AC,AB⊥AD,∠CAE=30°,则cos∠FCB=.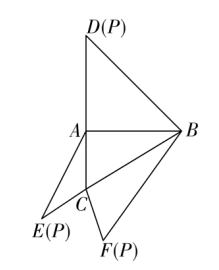
14. 将函数y= 的图象向右平移 个单位长度,则平移后的图象中与y轴最近的对称轴的方程是.15. 已知 = ,则 的值是.16. 若函数 的最大值为2,则常数 的一个取值为 .17. 已知tanθ=2,则cos2θ=;tan(θ﹣ )= .四、解答题
-
18. 在① ,② ,③ 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求 的值;若问题中的三角形不存在,说明理由.
问题:是否存在 ,它的内角 的对边分别为 ,且 , , ▲ ?
注:如果选择多个条件分别解答,按第一个解答计分.
19. △ABC的内角A,B,C的对边分别为a,b,c,已知 .(1)、求A;(2)、若 ,证明:△ABC是直角三角形.20. 的内角A,B,C的对边分别为a,b,c.已知B=150°.(1)、若a= c,b=2 ,求 的面积;(2)、若sinA+ sinC= ,求C.21. 已知函数f(x)=sin2xsin2x.(1)、讨论f(x)在区间(0,π)的单调性;(2)、证明: ;(3)、设n∈N*,证明:sin2xsin22xsin24x…sin22nx≤ .22. 中,sin2A-sin2B-sin2C=sinBsinC.(1)、求A;(2)、若BC=3,求 周长的最大值.23. 在 中,角 所对的边分别为 .已知 .(Ⅰ)求角C的大小;
(Ⅱ)求 的值;
(Ⅲ)求 的值.
-