2020年高考数学真题分类汇编专题08：导数在函数中的应用

试卷更新日期：2020-07-27 类型：二轮复习

进入出卷网下载

一、单选题

1. 若直线l与曲线y= $\sqrt{x}$ 和x²+y²= $\frac{1}{5}$ 都相切，则l的方程为（）

A、y=2x+1 B、y=2x+ $\frac{1}{2}$ C、y= $\frac{1}{2}$ x+1 D、y= $\frac{1}{2}$ x+ $\frac{1}{2}$

查看试题解析
2. 函数 $f (x) = x^{4} - 2 x^{3}$ 的图像在点 $(1 ， f (1))$ 处的切线方程为（）

A、 $y = - 2 x - 1$ B、 $y = - 2 x + 1$ C、 $y = 2 x - 3$ D、 $y = 2 x + 1$

查看试题解析

二、填空题

3. 设函数 $f (x) = \frac{e^{x}}{x + a}$ ．若 $f^{'} (1) = \frac{e}{4}$ ，则a= ．

查看试题解析
4. 曲线 $y = \ln x + x + 1$ 的一条切线的斜率为2，则该切线的方程为.

查看试题解析

三、解答题

5. 已知函数 $f (x) = x^{3} - k x + k^{2}$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、若 $f (x)$ 有三个零点，求k的取值范围．

查看试题解析
6. 设函数 $f (x) = x^{3} + b x + c$ ，曲线 $y = f (x)$ 在点( $\frac{1}{2}$ ，f( $\frac{1}{2}$ ))处的切线与y轴垂直．

(1)、求b．

(2)、若 $f (x)$ 有一个绝对值不大于1的零点，证明： $f (x)$ 所有零点的绝对值都不大于1．

查看试题解析
7. 已知函数f（x）=2lnx+1．

(1)、若f（x）≤2x+c，求c的取值范围；

(2)、设a>0时，讨论函数g（x）= $\frac{f (x) - f (a)}{x - a}$ 的单调性．

查看试题解析
8. 已知函数 $f (x) = e^{x} - a (x + 2)$ .

(1)、当 $a = 1$ 时，讨论 $f (x)$ 的单调性；

(2)、若 $f (x)$ 有两个零点，求a的取值范围.

查看试题解析
9. 已知函数 $f (x) = e^{x} + a x^{2} - x$ .

(1)、当a=1时，讨论f（x）的单调性；

(2)、当x≥0时，f（x）≥ $\frac{1}{2}$ x³+1，求a的取值范围.

查看试题解析
10. 已知函数 $f (x) = a e^{x - 1} - \ln x + \ln a$ ．

(1)、当 $a = e$ 时，求曲线y=f（x）在点（1，f（1））处的切线与两坐标轴围成的三角形的面积；

(2)、若f（x）≥1，求a的取值范围．

查看试题解析
11. 已知函数 $f (x) = x^{3} + k \ln x (k \in R)$ ， $f^{'} (x)$ 为 $f (x)$ 的导函数．
（Ⅰ）当 $k = 6$ 时，

（i）求曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

（ii）求函数 $g (x) = f (x) - f^{'} (x) + \frac{9}{x}$ 的单调区间和极值；

（Ⅱ）当 $k ⩾ - 3$ 时，求证：对任意的 $x_{1} ， x_{2} \in [1 ， + \infty)$ ，且 $x_{1} > x_{2}$ ，有 $\frac{f^{'} (x_{1}) + f^{'} (x_{2})}{2} > \frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}}$ ．

查看试题解析
12. 某地准备在山谷中建一座桥梁，桥址位置的竖直截面图如图所示：谷底O在水平线MN上、桥AB与MN平行， $O O^{'}$ 为铅垂线( $O^{'}$ 在AB上).经测量，左侧曲线AO上任一点D到MN的距离 $h_{1}$ (米)与D到 $O O^{'}$ 的距离a(米)之间满足关系式 $h_{1} = \frac{1}{40} a^{2}$ ；右侧曲线BO上任一点F到MN的距离 $h_{2}$ (米)与F到 $O O^{'}$ 的距离b(米)之间满足关系式 $h_{2} = - \frac{1}{800} b^{3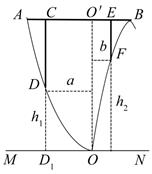} + 6 b$ .已知点B到 $O O^{'}$ 的距离为40米.

(1)、求桥AB的长度；

(2)、计划在谷底两侧建造平行于 $O O^{'}$ 的桥墩CD和EF，且CE为80米，其中C，E在AB上(不包括端点).桥墩EF每米造价k(万元)、桥墩CD每米造价 $\frac{3}{2} k$ (万元)(k>0).问 $O^{'} E$ 为多少米时，桥墩CD与EF的总造价最低?

查看试题解析
13. 已知关于x的函数 $y = f (x) ， y = g (x)$ 与 $h (x) = k x + b (k ， b \in R)$ 在区间D上恒有 $f (x) \geq h (x) \geq g (x)$ ．

(1)、若 $f (x) = x^{2} + 2 x ， g (x) = - x^{2} + 2 x ， D = (- \infty ， + \infty)$ ，求h(x)的表达式；

(2)、若 $f (x) = x^{2} - x + 1 ， g (x) = k \ln x ， h (x) = k x - k ， D = (0 ， + \infty)$ ，求k的取值范围；

(3)、若 $f (x) = x^{4} - 2 x^{2} ， g (x) = 4 x^{2} - 8 ， h (x) = 4 (t^{2} - t) x - 3 t^{4} + 2 t^{2} (0 < | t | \leq \sqrt{2}) ，$ $D = [m ， n] \subseteq [- \sqrt{2} ， \sqrt{2}] ，$ 求证： $n - m \leq \sqrt{7}$ ．

查看试题解析
14. 已知函数 $f (x) = 12 - x^{2}$ ．
（Ⅰ）求曲线 $y = f (x)$ 的斜率等于 $- 2$ 的切线方程；

（Ⅱ）设曲线 $y = f (x)$ 在点 $(t ， f (t))$ 处的切线与坐标轴围成的三角形的面积为 $S (t)$ ，求 $S (t)$ 的最小值．

查看试题解析
15. 已知1＜a≤2，函数f（x）＝e^x﹣x﹣a，其中e＝2.71828…为自然对数的底数．
（Ⅰ）证明：函数y＝f（x）在（0，+∞）上有唯一零点；

（Ⅱ）记x₀为函数y＝f（x）在（0，+∞）上的零点，证明：

（ⅰ） $\sqrt{a - 1}$ ≤x₀≤ $\sqrt{2 (a - 1)}$ ；

（ⅱ）x₀f（ $e^{x_{0}}$ ）≥（e﹣1）（a﹣1）a．

查看试题解析