初中数学浙教版八年级上册第二章 特殊三角形 单元检测(提高篇)
试卷更新日期:2020-07-26 类型:单元试卷
一、单选题
-
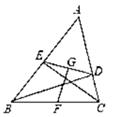
1. 下列定理中逆定理不存在的是( )A、全等三角形的对应角相等 B、如果在一个三角形中,两边相等,那么它们所对的角也相等 C、同位角相等,两直线平行 D、角平分线上的点到这个角的两边的距离相等2. 如图,△ABC中,BC=18,若BD⊥AC于D点,CE⊥AB于E点,F,G分别为BC、DE的中点,若ED=10,则FG的长为( )
 A、 B、 C、8 D、93. 如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B。下列结论中不一定成立的是( )
A、 B、 C、8 D、93. 如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B。下列结论中不一定成立的是( ) A、PA=PB B、PO平分∠APB C、OA=OB D、AB垂直平分OP4. 如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )
A、PA=PB B、PO平分∠APB C、OA=OB D、AB垂直平分OP4. 如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( ) A、140° B、100° C、50° D、40°5. 如图,在3×3的网格中,与ABC成轴对称,顶点在格点上,且位置不同的三角形有( )
A、140° B、100° C、50° D、40°5. 如图,在3×3的网格中,与ABC成轴对称,顶点在格点上,且位置不同的三角形有( ) A、5个 B、6个 C、7个 D、8个6. 如图:D,E分别是△ABC的边BC、AC上的点,若AB=AC,AD=AE,则( )
A、5个 B、6个 C、7个 D、8个6. 如图:D,E分别是△ABC的边BC、AC上的点,若AB=AC,AD=AE,则( ) A、当∠B为定值时,∠CDE为定值 B、当∠α为定值时,∠CDE为定值 C、当∠β为定值时,∠CDE为定值 D、当∠γ为定值时,∠CDE为定值7. 如图,P为∠AOB内一定点,M、N分别是射线OA,OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )
A、当∠B为定值时,∠CDE为定值 B、当∠α为定值时,∠CDE为定值 C、当∠β为定值时,∠CDE为定值 D、当∠γ为定值时,∠CDE为定值7. 如图,P为∠AOB内一定点,M、N分别是射线OA,OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( ) A、40° B、45° C、50° D、55°8. 如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,若△PMN周长的最小值是6 cm,则∠AOB的度数是( )
A、40° B、45° C、50° D、55°8. 如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,若△PMN周长的最小值是6 cm,则∠AOB的度数是( )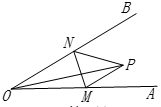 A、15 B、30 C、45 D、609. 勾股定理是人类最伟大的科学发现之一,在我国古代算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内.若知道图中阴影部分的面积,则一定能求出( )
A、15 B、30 C、45 D、609. 勾股定理是人类最伟大的科学发现之一,在我国古代算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内.若知道图中阴影部分的面积,则一定能求出( )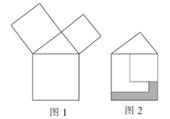 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和10. 如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和10. 如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )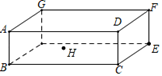 A、 B、17 C、 D、
A、 B、17 C、 D、二、填空题
-
11. 定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2 时,称点M为PQ的等高点”,称此时MP+MQ的值为PQ的“等高距离”.已知P(1,2),Q(3,4),当PQ的“等高距离”最小时,则点M的坐标为.12. 在如图所示的三角形中,∠A=30°,点P和点Q分别是边AC和BC上的两个动点,分别连接BP和PQ,把△ABC分割成三个三角形△ABP,△BPQ,△PQC,若分割成的这三个三角形都是等腰三角形,则∠C有可能的值有个.
 13. 如图,在四边形ABCE中,∠ABC=45°,AE=CE,连接AC,∠ACB=30°,过A作AD⊥AE交BC于D,若AD=AE,则 =。
13. 如图,在四边形ABCE中,∠ABC=45°,AE=CE,连接AC,∠ACB=30°,过A作AD⊥AE交BC于D,若AD=AE,则 =。 14. 下列命题中,逆命题是真命题的是(只填写序号)。
14. 下列命题中,逆命题是真命题的是(只填写序号)。①直角三角形两条直角边的平方和等于斜边的平方;
②等腰三角形两腰的高线相等;
③若三条线段a,b,c是三角形的三边,则这三条线段满足a+b>c
④角的内部,到角两边距离相等的点在这个角的平分线上,
⑤全等三角形的面积相等;
15. 在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得的锐角为46°,则底角∠B的大小为 .16. 定义:到三角形两边距离相等的点叫做三角形的准内心.已知在Rt△ABC中,∠C=90°,AC=6,BC=8,点P是△ABC的准内心(不包括顶点),且点P在△ABC的某条边上,则CP的长为。三、综合题
-
17. 已知:如图,△AOB的顶点O在直线
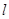 上,且AO=AB.
上,且AO=AB.  (1)、画出△AOB关于直线
(1)、画出△AOB关于直线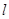 成轴对称的图形△COD,且使点A的对称点为点C; (2)、在(1)画出的图形中,AC与BD的位置关系是;(3)、在(1)画出的图形中连接AD,如果∠ABD=2∠ADB.
成轴对称的图形△COD,且使点A的对称点为点C; (2)、在(1)画出的图形中,AC与BD的位置关系是;(3)、在(1)画出的图形中连接AD,如果∠ABD=2∠ADB.求证:△AOC是等边三角形,并直接写出∠DAO∶∠DAB的值.
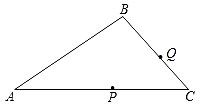
18. 已知,△ABC,AD⊥BD于点D,AE⊥CE于点E,连接DE. (1)、如图1,若BD,CE分别为△ABC的外角平分线,求证:DE= (AB+BC+AC).(2)、如图2,若BD,CE分别为△ABC的内角平分线,(1)中的结论成立吗?若成立请说明理由;若不成立,请猜想出新的结论并证明;(3)、如图3,若BD,CE分别为△ABC的一个内角和一个外角的平分线,AB=8,BC=10,AC=7,请直接写出DE的长为.19. 如图,在 中, , , 交 于点 .动点 从点 出发,按 的路径运动,且速度为 ,设出发时间为 .
(1)、如图1,若BD,CE分别为△ABC的外角平分线,求证:DE= (AB+BC+AC).(2)、如图2,若BD,CE分别为△ABC的内角平分线,(1)中的结论成立吗?若成立请说明理由;若不成立,请猜想出新的结论并证明;(3)、如图3,若BD,CE分别为△ABC的一个内角和一个外角的平分线,AB=8,BC=10,AC=7,请直接写出DE的长为.19. 如图,在 中, , , 交 于点 .动点 从点 出发,按 的路径运动,且速度为 ,设出发时间为 .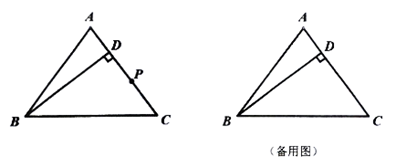 (1)、求 的长.(2)、当 时,求证: .(3)、当点 在 边上运动时,若 是以 为腰的等腰三角形,求出所有满足条件的 的值.(4)、在整个运动过程中,若 ( 为正整数),则满足条件的 的值有个.
(1)、求 的长.(2)、当 时,求证: .(3)、当点 在 边上运动时,若 是以 为腰的等腰三角形,求出所有满足条件的 的值.(4)、在整个运动过程中,若 ( 为正整数),则满足条件的 的值有个.
20. 在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG. (1)、求∠DFG的度数;(2)、设∠BAD=θ,
(1)、求∠DFG的度数;(2)、设∠BAD=θ,①当θ为何值时,△DFG为等腰三角形;
②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.
21. 请阅读下列材料问题:如图1,点A、B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小,小明的思路是:如图2所示,先作点A关于直线l的对称点A',使点A'、B分别位于直线l的两侧,再连接A'B,根据“两点间线段最短”可知A'B与直线l的交点P即为所求.
 (1)、如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D,若CP=1,AC=1,PD=2,求出AP+BP的值:(2)、将(1)中的条件“AC=1”去掉,换成“BD=4-AC”,其它条件不变,直接写出此时AP+BP的值:(3)、请结合图形,求 的最小值.22. 把三根长为3cm、4cm和5cm的细木棒首尾相连,能搭成一个直角三角形.(1)、如果把这三根细木棒的长度分别扩大为原来的a倍(a>1),那么所得的三根细木棒能不能搭成一个直角三角形, 为什么?(2)、如果把这三根细木棒的长度分别延长x cm(x>0),那么所得的三根细木棒还能搭成一个三角形吗?为什么?如果能,请判断这个三角形的形状(锐角三角形、直角三角形还是钝角三角形),并说明理由.23. 在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
(1)、如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D,若CP=1,AC=1,PD=2,求出AP+BP的值:(2)、将(1)中的条件“AC=1”去掉,换成“BD=4-AC”,其它条件不变,直接写出此时AP+BP的值:(3)、请结合图形,求 的最小值.22. 把三根长为3cm、4cm和5cm的细木棒首尾相连,能搭成一个直角三角形.(1)、如果把这三根细木棒的长度分别扩大为原来的a倍(a>1),那么所得的三根细木棒能不能搭成一个直角三角形, 为什么?(2)、如果把这三根细木棒的长度分别延长x cm(x>0),那么所得的三根细木棒还能搭成一个三角形吗?为什么?如果能,请判断这个三角形的形状(锐角三角形、直角三角形还是钝角三角形),并说明理由.23. 在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N. (1)、如图①,若△AMN是等边三角形,则∠BAC=°;(2)、如图②,若∠BAC=135°,求证:BM2+CN2=MN2.(3)、如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.
(1)、如图①,若△AMN是等边三角形,则∠BAC=°;(2)、如图②,若∠BAC=135°,求证:BM2+CN2=MN2.(3)、如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.