初中数学浙教版八年级上册第二章 特殊三角形 单元检测(基础篇)
试卷更新日期:2020-07-26 类型:单元试卷
一、单选题
-
1. 在一些美术字中,有的汉字是轴对称图形.下面 个汉字中,可以看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 我们知道,平面内不垂直的两条相交直线是轴对称图形,该图形对称轴条数为( )A、1 B、2 C、4 D、无数3. 已知等腰三角形的一个角为72°,则其顶角为( )A、36° B、45° C、60° D、72°或36°4. 下列线段不能组成直角三角形的是( )A、a=3,b=4,c=5 B、a=1,b= ,c= C、a=2,b=3,c=4 D、a=7,b=24,c=255. 如图,在△ABC中,AB=AC,分别以点A点、B为圆心,以大于 长为半径画弧,两弧交点的连线交AC于点D,交AB于点E,连接BD,若 ,则 ( )
2. 我们知道,平面内不垂直的两条相交直线是轴对称图形,该图形对称轴条数为( )A、1 B、2 C、4 D、无数3. 已知等腰三角形的一个角为72°,则其顶角为( )A、36° B、45° C、60° D、72°或36°4. 下列线段不能组成直角三角形的是( )A、a=3,b=4,c=5 B、a=1,b= ,c= C、a=2,b=3,c=4 D、a=7,b=24,c=255. 如图,在△ABC中,AB=AC,分别以点A点、B为圆心,以大于 长为半径画弧,两弧交点的连线交AC于点D,交AB于点E,连接BD,若 ,则 ( )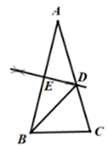 A、 B、 C、 D、6. 已知∠AOB=30°,点P在∠AOB的内部,点P1和点P关于OA对称,点P2和点P关于OB对称,则P1、O、P2三点构成的三角形是( )A、直角三角形 B、钝角三角形 C、等腰直角三角形 D、等边三角形7. 下列定理中,没有逆定理的是( )A、同旁内角互补,两直线平行 B、直角三角形的两锐角互余 C、互为相反数的两个数的绝对值相等 D、同位角相等,两直线平行8. 如图,三角形ABC,∠BAC= ,AD是三角形ABC的高,图中相等的是( ).
A、 B、 C、 D、6. 已知∠AOB=30°,点P在∠AOB的内部,点P1和点P关于OA对称,点P2和点P关于OB对称,则P1、O、P2三点构成的三角形是( )A、直角三角形 B、钝角三角形 C、等腰直角三角形 D、等边三角形7. 下列定理中,没有逆定理的是( )A、同旁内角互补,两直线平行 B、直角三角形的两锐角互余 C、互为相反数的两个数的绝对值相等 D、同位角相等,两直线平行8. 如图,三角形ABC,∠BAC= ,AD是三角形ABC的高,图中相等的是( ).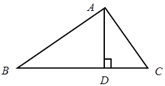 A、∠B=∠C B、∠BAD=∠B C、∠C=∠BAD D、∠DAC=∠C9. 如图,在四边形ABCD中,∠DAB=90°,∠DCB=90°,E、F分别是BD、AC的中点,AC=6,BD=10,则EF的长为( )
A、∠B=∠C B、∠BAD=∠B C、∠C=∠BAD D、∠DAC=∠C9. 如图,在四边形ABCD中,∠DAB=90°,∠DCB=90°,E、F分别是BD、AC的中点,AC=6,BD=10,则EF的长为( ) A、3 B、4 C、5 D、10. 如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A、3 B、4 C、5 D、10. 如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( ) A、AC=AD B、AC=BC C、∠ABC=∠ABD D、∠BAC=∠BAD
A、AC=AD B、AC=BC C、∠ABC=∠ABD D、∠BAC=∠BAD二、填空题
-
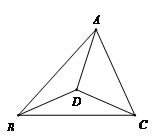
11. 若点M(﹣3,b)与点N(a,2)关于x轴对称,则a+b=.12. 已知等腰三角形的其中两边长为6cm和8cm,则这个三角形的周长为cm.13. 如图,在△ABC内,三边垂直平分线交点为D,若∠BAC=50°,则∠BDC的度数为 .
 14. 如图,四边形ABCD中,∠A = ∠B = 90°,AB边上有一点E,CE,DE分别是∠BCD和∠ADC 的角平分线,如果ABCD的面积是12,CD = 8,那么AB的长度为.
14. 如图,四边形ABCD中,∠A = ∠B = 90°,AB边上有一点E,CE,DE分别是∠BCD和∠ADC 的角平分线,如果ABCD的面积是12,CD = 8,那么AB的长度为. 15. 已知命题“线段垂直平分线上的任意一点到这条线段两个端点的距离相等”,用“如果…,那么…”的形式写出它的逆命题,并判断其真假.逆命题: . 这个逆命题是 命题(填“真”或“假”).16. 如图, 中, 为斜边中点, 为斜边上的高,若 , ,则 的面积是.
15. 已知命题“线段垂直平分线上的任意一点到这条线段两个端点的距离相等”,用“如果…,那么…”的形式写出它的逆命题,并判断其真假.逆命题: . 这个逆命题是 命题(填“真”或“假”).16. 如图, 中, 为斜边中点, 为斜边上的高,若 , ,则 的面积是.
三、解答题
-
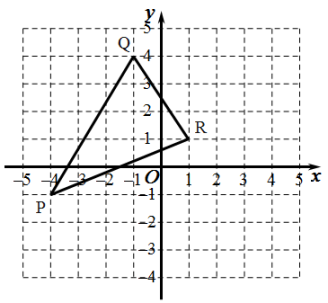
17. 如图,请作出△PQR关于y轴对称的△P1Q1R1 , 写出它们的坐标P1 , Q1 , R1
 18. 在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
18. 在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)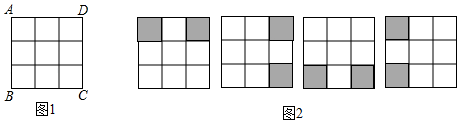
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
 19. 如图,在△ABC中,已知AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=125°.求∠ACB和∠BAC的度数.
19. 如图,在△ABC中,已知AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=125°.求∠ACB和∠BAC的度数. 20. 已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD
20. 已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD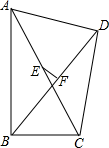 21. 图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,点A、B、M、N均落在格点上,在图①、图②给定的网格中按要求作图.
21. 图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,点A、B、M、N均落在格点上,在图①、图②给定的网格中按要求作图.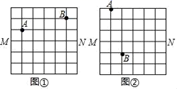 (1)、在图①中的格线MN上确定一点P,使PA与PB的长度之和最小(2)、在图②中的格线MN上确定一点Q,使∠AQM=∠BQM.
(1)、在图①中的格线MN上确定一点P,使PA与PB的长度之和最小(2)、在图②中的格线MN上确定一点Q,使∠AQM=∠BQM.要求:只用无刻度的直尺,保留作图痕迹,不要求写出作法.
22. 如图,在△ABC中,∠ACB=90°,AC=BC,D为BC边的中点,BE⊥AB交AD的延长线于点E,CF平分∠ACB交AD于点F,连接CE。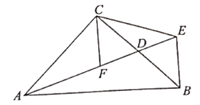
求证:
(1)、点D是EF的中点;(2)、△CEF是等腰三角形。23. 如图,一轮船以40km/h的速度由西向东航行,在途中点C处接到台风警报,台风中心点B正以20km/h的速度由南向北移动.已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.(假定轮船不改变航向).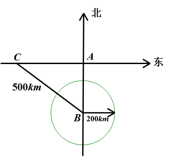 (1)、如果这艘轮船不改变航向,经过11小时,轮船与台风中心相距多远?此时,轮船是否受到台风影响?(2)、如果这艘轮船受到台风影响,请求出轮船受到台风影响一共经历了多少小时?24. 如图,在 中, , ,AD是 的角平分线, ,垂足为E.
(1)、如果这艘轮船不改变航向,经过11小时,轮船与台风中心相距多远?此时,轮船是否受到台风影响?(2)、如果这艘轮船受到台风影响,请求出轮船受到台风影响一共经历了多少小时?24. 如图,在 中, , ,AD是 的角平分线, ,垂足为E.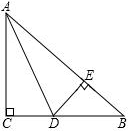 (1)、求证: ;(2)、已知 ,求AC的长;(3)、求证: .
(1)、求证: ;(2)、已知 ,求AC的长;(3)、求证: .