初中数学浙教版八年级上册2.7 探索勾股定理（2）同步练习

试卷更新日期：2020-07-26 类型：同步测试

进入出卷网下载

一、单选题

1. 判断以下各组线段为边作三角形，可以构成直角三角形的是（）

A、6，15，17 B、7，12，15 C、13，15，20 D、7，24，25

查看试题解析
2. 下列说法不能得到直角三角形的（）

A、三个角度之比为 1：2：3 的三角形 B、三个边长之比为 3：4：5 的三角形 C、三个边长之比为 8：16：17 的三角形 D、三个角度之比为 1：1：2 的三角形

查看试题解析
3. 下列三角形中，不是直角三角形的是（）

A、△ABC中，∠A=∠B-∠C B、△ABC中，a：b：c=1：2：3 C、△ABC中，a²=c²-b² D、△ABC中，三边的长分别为m²+n² ， m²-n² ， 2mn(m>n>0)

查看试题解析
4. 将直角三角形的各边都缩小或扩大同样的倍数后，得到的三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、不确定

查看试题解析
5. 已知三角形三边的长分别为3、2、 $\sqrt{5}$ ，则该三角形的形状是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

查看试题解析
6. 如图，已知 $△ A B C$ 中， $A B = 10 ， A C = 8 ， B C = 6 ， A B$ 的垂直平分线分别交 $A C ， A B$ 于 $D ， E ，$ 连接 $B D$ ，则 $C D$ 的长为（）

A、 $1$ B、 $\frac{5}{4}$ C、 $\frac{7}{4}$ D、 $\frac{25}{4}$

查看试题解析
7. $Δ A B C$ 的三边分别为a，b，c，下列条件：① $∠ A = ∠ B - ∠ C$ ；② $a^{2} = (b + c) (b - c)$ ；③ $a ： b ： c = 3 ： 4 ： 5$ .其中能判断 $Δ A B C$ 是直角三角形的条件个数有 $($ $)$

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 在四边形 $A B C D$ 中， $∠ B = 90^{°} ， A B = B C = 1 ， C D = \sqrt{6} ， A D = 2$ ，若 $∠ D = α$ ，则 $∠ B C D$ 的大小为（）

A、 $2 α$ B、 $90^{°} + α$ C、 $135^{°} - α$ D、 $180^{°} - α$

查看试题解析
9. $△ A B C$ 的三边 $B C = a ， A C = b ， A B = c$ ，且 $(a + c) (a - c) - b^{2} = 0$ ，下列结论正确的是（）

A、 $△ A B C$ 是等腰直角三角形且 $∠ C = 90 °$ B、 $△ A B C$ 是直角三角形或等腰三角形 C、 $△ A B C$ 是直角三角形，且 $∠ C = 90 °$ D、 $△ A B C$ 是直角三角形，且 $∠ A = 90 °$

查看试题解析
10. 我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题的大意是：有一块三角形沙田，三条边长分别为5里；12里；13里，问这块沙田面积有多大？题中的1里=0.5千米，则该沙田的面积为（）

A、3平方千米 B、7.5平方千米 C、15平方千米 D、30平方千米

查看试题解析

二、填空题

11. 已知a、b、c是△ABC三边的长，且满足关系式 $\sqrt{c^{2} + a^{2} - b^{2}} +$ | $c - a$ |=0，则△ABC的形状是．

查看试题解析
12. 一个三角形的三边长的比为3：4：5，且其周长为60cm，则其面积为．

查看试题解析
13. 如图所示的网格是正方形网格，则 $∠ A C B - ∠ D C E =$ $°$ （点 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 是网格线交点）．

查看试题解析
14. 在△ABC 中，若 $a^{2} + b^{2} = 25 ， a^{2} - b^{2} = 7 ， c = 5$ ，则最长边上的高为．

查看试题解析
15. 已知a，b，c为三角形的三边，且满足a²c²-b²c²=a⁴-b⁴ ，那么它的形状是．

查看试题解析

三、解答题

16. 如图，在 $△ A B C$ 中， $A B = 6$ ， $A C = 8$ ， $B C = 10$ ， $B C$ 的垂直平分线分别交 $A C$ 、 $B C$ 于点 $D$ 、 $E$ ，求 $C D$ 的长．

查看试题解析
17. 如图，四边形 $A B C D$ 中， $A B = 3$ ， $B C = 4$ ， $C D = 12$ ， $A D = 13$ ，且 $∠ B = 90 °$ ，求四边形 $A B C D$ 的面积．

查看试题解析
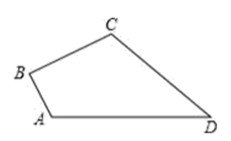18. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中 $A B = B C$ ，由于某种原因，由C到B的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点D(A、D、B)在同一条直线上)，并新修一条路CD，测得 $C A = 6.5$ 千米， $C D = 6$ 千米， $A D = 2.5$ 千米.

(1)、问CD是否为从村庄C到河边最近的路？请通过计算加以说明：

(2)、求原来的路线 $B C$ 的长.

查看试题解析
19. 在如图所示的网格中有四条线段AB、CD、EF、GH（线段端点在格点上），

(1)、选取其中三条线段，使得这三条线段能围成一个直角三角形.
答：选取的三条线段为.

(2)、只变动其中两条线段的位置，在原图中画出一个满足上题的直角三角形（顶点仍在格点，并标上必要的字母）.
答：画出的直角三角形为△.

(3)、所画直角三角形的面积为.

查看试题解析