初中数学浙教版八年级上册2.6 直角三角形（1）同步练习
试卷更新日期：2020-07-26 类型：同步测试
一、单选题
-
1. 如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，CD是斜边AB上的高，AD＝3 cm，则AB的长度是（ ）
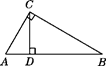A、3cm B、6cm C、9cm D、12cm2. 如图，在△ABC中，∠ACB=90°，CD是AB边上的高线，图中与∠A互余的角有（ ）
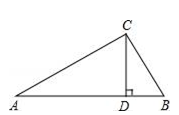A、0个 B、1个 C、2个 D、3个3. 如图，一根竹竿AB，斜靠在竖直的墙上，P是AB中点，A'B'表示竹竿AB端沿墙上、下滑动过程中的某个位置，则在竹竿AB滑动过程中OP（ ）
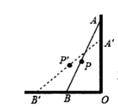A、下滑时，OP增大 B、上升时，OP减小 C、无论怎样滑动，OP不变 D、只要滑动，OP就变化4. 如图所示，已知∠1=∠2，AD=BD=4，CE⊥AD，2CE=AC，那么CD的长是（ ）
A、2 B、3 C、1 D、1.55. 如果一个三角形的三边长分别为 3、4、5 ，那么它的斜边上的高为（ ）
A、 B、 C、 D、6. 如图，Rt△ACB中，∠ACB=90°，∠A=60°，CD，CE分别是△ABC的高和中线，下列说法错误的是（ ）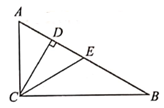
A、AD=DE B、S△CEB=S△ACE C、AC，BC的垂直平分线都经过点E D、图中只有一个等腰三角形7. 如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开，若测得AM的长为1.2km，则M、C两点间的距离为（ ）
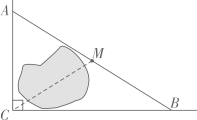A、0.5km B、0.6km C、0.9km D、1.2km8. 如图，在 中， 是 上一点， ， ， 分别是 ， 的中点， ，则 的长为（ ）
A、3 B、4 C、5 D、69. 如图， 中， ， ， 平分 交 于点 ，点 为 的中点，连接 ，则 的周长为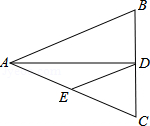
A、20 B、12 C、14 D、1310. 如图，∠ABC=∠ADC=90°，E是AC的中点，则（ ）
A、∠1＞∠2 B、∠1=∠2 C、∠1＜∠2 D、∠1与∠2大小关系不能确定二、填空题
-
11. 如图，在△ABC中，∠ACB=90°，∠ABC=60°，BD平分∠ABC，P点是BD的中点，若AD=10，则CP的长为.
12. 在Rt
ABC中，∠C=90°，∠A=65°，则∠B=. 13. 如图，已知AB是Rt△ABC和Rt△ABD的斜边，O是AB的中点，其中OC是2 cm，则OD＝.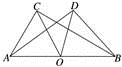
14. 如图：在 中，CD是斜边AB上的中线，若 ，则 ．
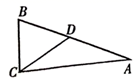15. 如图，已知在 中， ，点D在边 上，且 ， .则 的度数为°．
三、解答题
-
16. 已知：如图， ， 分别是 、 的中点. 求证： .
17. 已知：如图，在△ABC中，D是BC上的点，AD=AB，E，F分别是AC，BD的中点，AC=6．求EF的长。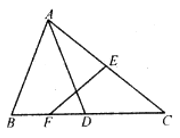
18. 如图，在△ABC中，∠B＝2∠C，AE平分∠BAC交BC于点E.
(1)、如图①，若AD⊥BC于点D，∠C＝40°，求∠DAE的度数；(2)、如图②，若EF⊥AE交AC于点F，求证：∠C＝2∠FEC.
