初中数学浙教版八年级上册2.4 等腰三角形的判定定理 同步练习
试卷更新日期：2020-07-26 类型：同步测试
一、单选题
-
1. 在 中， ，若 ，则 的形状为（ ）A、钝角三角形 B、等边三角形 C、直角三角形 D、不等边三角形2. 下列不能断定 为等边三角形的是（ ）A、 ， B、 C、 ， D、 ，3. 在△ABC中，∠A：∠B：∠C＝2：2：5，则△ABC是（ ）A、等腰三角形 B、等边三角形 C、直角三角形 D、锐角三角形4. 已知：在△ABC中，∠A=60°，如要判定△ABC是等边三角形，还需添加一个条件．现有下面三种说法：
①如果添加条件“AB=AC”，那么△ABC是等边三角形；
②如果添加条件“∠B=∠C”，那么△ABC是等边三角形；
③如果添加条件“边AB、BC上的高相等”，那么△ABC是等边三角形．
上述说法中，正确的有（ ）
A、3个 B、2个 C、1个 D、0个5. 如图， ， ， ，若 ，则 （ ）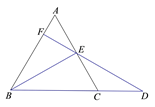
A、 B、 C、 D、6. 有下列命题：①等腰三角形的角平分线、中线和高重合；②等腰三角形两腰上的高相等；③有个外角等于120°的等腰三角形是等边三角形；④等边三角形的高线、中线、角平分线都相等；其中正确的有（ ）A、1个 B、2个 C、3个 D、4个7. 如图，在△ABC 中，∠BAC＝72°，∠C＝36°，∠BAC 的平分线 AD 交 BC 于 D， 则图中有等腰三角形（ ）
A、0 个 B、1 个 C、2 个 D、3 个8. 具备下列条件的三角形为等腰三角形的是（ ）A、有两个角分别为20°，120° B、有两个角分别为40°，80° C、有两个角分别为30°，60° D、有两个角分别为50°，80°9. 如果一个三角形的外角平分线与这个三角形的一边平行，则这个三角形一定是（ ）A、等腰三角形 B、等边三角形 C、等腰直角三角形 D、无法确定10. 如图，在6×6的正方形网格中，点A ， B均在正方形格点上，若在网格中的格点上找一点C ， 使△ABC为等腰三角形，这样的点C一共有（ ）
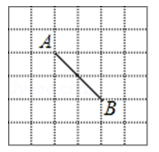
A、7个 B、8个 C、10个 D、12个二、填空题
-
11. 已知△ABC中，∠A=∠B=60°，AB=5cm，则△ABC的周长为 .12. 如图，在 中， ， 平分 ，作 ，交 的延长线于点 ，则 是三角形.
13. 如图已知OA=a，P是射线ON上一动点，∠AON=60°，当OP=时，△AOP为等边三角形．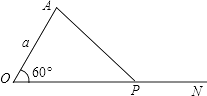
14. 如图，在三角形ABC中，DE垂直平分BC，交BC、AB分别于 D、E，连接CE，BF平分∠ABC，交CE于F，若BE=AC，∠ACF=16°，则∠EFB=
15. 如图，在△ABC中，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于点E、F.当EF=6，BE=4时，CF的长为.
三、解答题
-
16. 如图，AB=AC，∠A=120º，BC=6cm，ED、FG分别是AB，AC的垂直平分线，求BE的长.
17. 如图，在△ABC中，∠ABC>60°，∠BAC<60°，以AB为边作等边△ABD(点C、D在边AB的同侧)，连接CD，
(Ⅰ)若∠ABC=90°，∠BAC=30°，求∠BDC的度数；
(Ⅱ)当∠BAC=2∠BDC时，请判断△ABC的形状并说明理由；
(Ⅲ)当∠BCD等于多少度时，∠BAC=2∠BDC恒成立。
18. 如图，△ABC中，AB＝AC，∠A＝36°．
(1)、用尺规作图作∠ABC的角平分线，交AC于点D；（保留作图痕迹，不写作法）．(2)、求证：△BCD是等腰三角形．19. 如图，在△ABC中，AB＝AC＝2，∠B＝∠C＝40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE＝40°，DE交线段AC于E．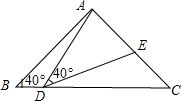
(1)、当∠BDA＝115°时，∠EDC＝°，∠DEC＝°；点D从B向C运动时，∠BDA逐渐变（填“大”或“小”）；(2)、当DC等于多少时，△ABD≌△DCE，请说明理由；(3)、在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数．若不可以，请说明理由．20. 如图，A、B、C在同一直线上，且△ABD，△BCE都是等边三角形，AE交BD于点M，CD交BE于点N，MN∥AC，求证：
(1)、∠BDN=∠BAM；(2)、△BMN是等边三角形．