初中数学浙教版八年级上册2.3 等腰三角形的性质定理（1）同步练习

试卷更新日期：2020-07-26 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 等边三角形的一个角是（    ）．
    A、30° B、60° C、45° D、90°

    查看试题解析

  • 2. 已知一个等腰三角形的底角为 50° ，则这个三角形的顶角为（    ）
    A、40° B、50° C、80° D、100°

    查看试题解析

  • 3. 在△ABC中，AB=AC，∠C=75°， 则∠A的度数是（   ）
    A、30° B、50° C、75° D、150°

    查看试题解析

  • 4. 如右上图，五角星的五个角都是顶角为36°的等腰三角形，则∠AMB的度数为（ ）

    A、144° B、120° C、108° D、100°

    查看试题解析

  • 5. 若等腰三角形的顶角为50°，则这个等腰三角形的底角度数为（    ）
    A、50° B、65° C、80° D、130°

    查看试题解析

  • 6. 如图，在△ABC中，点D在BC上，AB=AD=DC，∠B=70°，则∠C的度数为（      ）

    A、30° B、35° C、40° D、45°

    查看试题解析

  • 7. 如图，△ABC是等边三角形，BD⊥AB，且AB=BD，则∠ACD的度数为（   ）

    A、30° B、35° C、45° D、50°

    查看试题解析

  • 8. 在等腰三角形ABC中，∠A=80°.则∠B的度数不可能为（   ）
    A、20° B、40° C、50° D、80°

    查看试题解析

  • 9. 如图，在 △ABC 中，DE是AB的垂直平分线，且分别交AB、AC于点D和E，  ∠A =50°，  ∠C =60°，则 ∠EBC 为（ ）

    A、30° B、20° C、25° D、35°

    查看试题解析

  • 10. 已知一个等腰三角形内角的度数之比为1：4，则它的顶角的度数为（ ）
    A、20° B、36° C、120° D、20°或120°

    查看试题解析

二、填空题

  • 11. 等腰三角形的一个内角是 100° ，则它的底角的度数为.

    查看试题解析

  • 12. 若等腰三角形的顶角为α，则一腰上的高线与另一腰的夹角是(用α的代数式表示)

    查看试题解析

  • 13. 如图，在△ABC中，AB=AC，外角∠ACD=110°，则∠A=.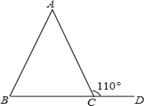

    查看试题解析

  • 14. 如图，已知 ∠AOD=30° ，点 C 是射线 OD 上的一个动点，在点 C 的运动过程中， △AOC 恰好是等腰三角形，则此时 ∠A 所有可能的度数为 ° .

    查看试题解析

  • 15. 如图， ΔABC 为等腰直角三角形， ∠ABC=90∘ ， ΔADB 为等边三角形，则 ∠ADC= .

    查看试题解析

三、解答题

  • 16. 已知如图，四边形 ABCD 中， AB=BC ， AD=CD ，求证： ∠BAD=∠BCD .

    查看试题解析

  • 17. 数学课上，张老师举了下面的例题：

    例1：等腰△ABC中，∠A=100°，求∠B的度数．(答案：40°)

    例2：等腰△ABC中，∠A=50°，求∠B的度数．(答案：50°或65°或80°)

    张老师启发同学们进行变式，小敏编了如下一题：

    变式：等腰△ABC中，∠A=70°，求∠B的度数．

    (1)、请你解答小敏编的变式题：
    (2)、解第(1)小题后小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同．如果在等腰△ABC中，设∠A=x°，当∠B有三个不同的度数时，请你探索x的取值范围．

    查看试题解析