初中数学浙教版九年级上册第二章 简单事件的概率 单元检测（提高篇）
试卷更新日期：2020-07-26 类型：单元试卷
一、单选题
-
1. 同时抛掷两枚质地均匀的正方体骰子（骰子每个面上的点数分别为1，2，3，4，5，6）．下列事件中是必然事件的是（ ）A、两枚骰子朝上一面的点数和为6 B、两枚骰子朝上一面的点数和不小于2 C、两枚骰子朝上一面的点数均为偶数 D、两枚骰子朝上一面的点数均为奇数2. 根据你对下列诗词的理解，请你从概率统计的角度判断：所给诗词描述的事件属于随机事件的是（ ）A、锄禾日当午，汗滴禾下土 B、白日依山尽，黄河入海流 C、离离原上草，一岁一枯荣 D、春眠不觉晓，处处闻啼鸟3. 某校九年级一班共有学生50人，现在对他们的生日（可以不同年）进行统计，则正确的说法是（ ）A、至少有两名学生生日相同 B、不可能有两名学生生日相同 C、可能有两名学生生日相同，但可能性不大 D、可能有两名学生生日相同，且可能性很大4. 如图所示，电路图上有A，B，C三个开关和一个小灯泡，闭合开关C或者同时闭合开关A、B，都可使小灯泡发光．现在任意闭合其中一个开关，则小灯泡发光的概率等于（ ）
A、 B、 C、 D、5. 定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”，如“947”就是一个“V数”.若十位上的数字为2，则从1，3，4，5中任选两数，能与2组成“V数”得概率是（ ）A、 B、 C、 D、6. “五一”长假期间，某玩具超市设立了一个如图所示的可以自由转动的转盘，开展有奖购买活动，顾客购买玩具就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应奖品．下表是该活动的一组统计数据：转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”区域的次数m
68
108
140
355
560
690
落在“铅笔”区域的频率
0.68
0.72
0.70
0.71
0.70
0.69
下列说法不正确的是（ ）
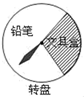A、当n很大时，估计指针落子在”铅笔“区域的概率大约是0.70 B、假如你去转动转盘一次，获得“铅笔”概率大约是0.70 C、如果转动转盘3000次，指针落在“文具盒”区域的次数大约有900次 D、转动转盘20次，一定有6次获得“文具盒”7. 某学习小组做抛掷一枚纪念币的实验，整理同学们获得的实验数据，如下表．抛掷次数
50
100
200
500
1000
2000
3000
4000
5000
“正面向上”的次数
19
38
68
168
349
707
1069
1400
1747
“正面向上”的频率
0.3800
0.3800
0.3400
0.3360
0.3490
0.3535
0.3563
0.3500
0.3494
下面有三个推断：①通过上述实验的结果，可以推断这枚纪念币有很大的可能性不是质地均匀的；②如果再次做此实验，仍按上表抛掷的次数统计数据，那么在数据表中，“正面向上”的频率有更大的可能仍会在0.35附近摆动；③在用频率估计概率时，用实验5000次时的频率0.3494一定比用实验4000次时的频率0.3500更准确．其中正确的是（ ）
A、①③ B、①② C、②③ D、①②③8. 如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是（ ）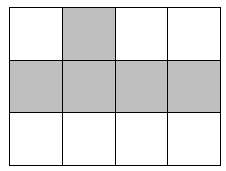
A、 B、 C、 D、9.在边长为1的小正方形组成的网格中，有如图所示的A，B两点，在格点上任意放置点C，恰好能使得△ABC的面积为1的概率为（ ）.
A、
B、
C、
D、
10. 甲乙两人轮流在黑板上写下不超过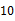
的正整数（每次只能写一个数），规定禁止在黑板上写已经写过的数的约数，最后不能写的为失败者，如果甲写第一个，那么，甲写数字（ ）时有必胜的策略．
A、10 B、9 C、8 D、6二、填空题
-
11. 写一个你喜欢的实数m的值，使得事件“对于二次函数 ，当 时，y随x的增大而增大”成为随机事件，这个实数m的值.12. 从甲地到乙地有A，B，C三条不同的公交线路．为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：
早高峰期间，乘坐（填“A”，“B”或“C”）线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．
13. 为了了解学生每月的零用钱情况，从甲、乙、丙三个学校各随机抽取200名学生，调查了他们的零用钱情况（单位：元）具体情况如下：学校频数零用钱
100≤x＜200
200≤x＜300
300≤x＜400
400≤x＜500
500以上
合计
甲
5
35
150
8
2
200
乙
16
54
68
52
10
200
丙
0
10
40
70
80
200
在调查过程中，从（填“甲”，“乙”或“丙”）校随机抽取学生，抽到的学生“零用钱不低于300元”的可能性最大．
14. 某水果公司新购进10000千克柑橘，每千克柑橘的成本为9元．柑橘在运输、存储过程中会有损坏，销售人员从所有的柑橘中随机抽取若干柑橘，进行“柑橘损坏率”统计，并把获得的数据记录如表所示：柑橘总重量n/千克
50
100
150
200
250
300
350
400
450
500
损坏柑橘重量m/千克
5.50
10.50
15.15
19.42
24.25
30.93
35.32
39.24
44.57
51.54
柑橘损坏的频率
0.110
0.105
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
根据表中数据，估计柑橘损坏的概率为（结果保留小数点后一位）；由此可知，去掉损坏的柑橘后，水果公司为了不亏本，完好柑橘每千克的售价至少为元．
15. 一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使不知道密码的人一次就拨对密码的概率小于 ，则密码的位数至少需要位。16. 将长度为8厘米的木棍截成三段，每段长度均为整数厘米．如果截成的三段木棍长度分别相同算作同一种截法（如：5，2，1和1，5，2），那么截成的三段木棍能构成三角形的概率是 ．三、解答题
-
17. 有三张正面分别写有数字1，3，4的卡片，它们的背面完全相同，将这三张卡片背面朝上洗匀后随机抽取一张，以其正面的数字作为a的值，把方程组 的解记为平面直角坐标系中点A的坐标(x，y)，求点A在第四象限的概率。18. 如图，在3 3的正方形网格中，点A、B、C、D、E、F都是格点.
(1)、从A、D、E、F四点中任意取一点，以所取点及B、C为顶点画三角形，那么所画三角形是等腰三角形的概率是.(2)、从A、D、E、F四点中任意取两点，以所取两点及B、C为顶点画四边形，求所画四边形是平行四边形的概率.（请用“画树状图”或“列表”等方式写出分析过程）19. 一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52
78
88
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56
(1)、请将表中数据补充完整，并画出折线统计图中剩余部分．
(2)、如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？(3)、在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？
20. 小红和小丁玩纸牌游戏，如图是同一副扑克中的4张牌的正面，将它们正面朝下洗匀后放在桌面上.
(1)、小红从4张牌中抽取一张，这张牌的数字为4的倍数的概率是；(2)、小红先从中抽出一张，小丁从剩余的3张牌中也抽出一张，把两人抽取的牌面上的数字相加.若为偶数，则小红获胜；若为奇数，则小丁获胜.请用画树状图或列表法的方法说明这个游戏规则对双方是否公平.21. 一个不透明的袋子中装有四个小球，上面分别标有数字-2，-1，0，1，它们除了数字不一样外，其它完全相同.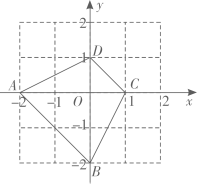
(1)、随机从袋子中摸出一个小球，摸出的球上面标的数字为正数的概率是.(2)、小聪先从袋子中随机摸出一个小球，记下数字作为点 的纵坐标，如图，已知四边形 的四个顶点的坐标分别为 ， ， ， ，请用画树状图或列表法，求点 落在四边形 所围成的部分内（含边界）的概率.22. 阅读对话，解答问题.
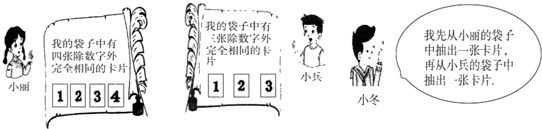(1)、分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字，请用树状图法或列表法写出（a，b）的所有取值；(2)、小冬抽出（a，b）中使关于x的一元二次方程x2﹣ax+2b＝0根为有理数的是小丽赢，方程的根为无理数的是小兵赢，你觉得游戏是否公平？若公平，请说明理由；若不公平，请修改游戏方案.23. 经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转．由于该十字路口右拐弯处是通往新建经济开发区的，因此交管部门在汽车行驶高峰时段对车流量作了统计，发现汽车在此十字路口向右转的频率为 ，向左转和直行的频率均为 .(1)、假设平均每天通过该路口的汽车为5000辆，求汽车在此左转、右转、直行的车辆各是多少辆；(2)、目前在此路口，汽车左转、右转、直行的绿灯亮的时间均为30秒，在绿灯总时间不变的条件下，为了缓解交通拥挤，请你利用概率的知识对此路口三个方向的绿灯亮的时间做出合理的调整．