初中数学浙教版九年级上册2.3 用频率估计概率 同步练习
试卷更新日期：2020-07-26 类型：同步测试
一、单选题
-
1. 投掷硬币m次，正面向上n次，其频率p= ，则下列说法正确的是（ ）A、p一定等于 B、p一定不等于 C、多投一次，p更接近 D、投掷次数逐步增加，p稳定在 附近2. 用频率估计概率，可以发现，抛掷硬币，“正面朝上”的概率为0.5，那么掷一枚质地均匀的硬币10次，下列说法正确的是（ ）A、每两次必有1次正面向上 B、可能有5次正面向上 C、必有5次正面向上 D、不可能有10次正面向上3. 做抛掷同一枚啤酒瓶盖的重复试验，经过统计得“凸面朝上”的频率约为0.44，则可以估计抛掷这枚啤酒瓶盖出现“凸面朝上”的概率约为（ ）A、22% B、44% C、50% D、56%4. 某足球运动员在同一条件下进行射门，结果如下表所示：
射门次数n
20
50
100
200
500
800
踢进球门频数m
13
35
58
104
255
400
踢进球门频率m/n
0.65
0.7
0.58
0.52
0.51
0.5
则该运动员射门一次，射进门的概率为（ ）
A、0.7 B、0.65 C、0.58 D、0.55. 在一个不透明的口袋中装有若干个颜色不同其余都相同的球，如果口袋中装有3个红球且摸到红球的频率为 ， 那么口袋中球的总个数为（ ）A、13 B、14 C、15 D、166. 某林业部门要考察某种幼树在一定条件下的移植成活率，下图是这种幼树在移植过程中成活情况的一组数据统计结果.下面三个推断：①当移植棵数是1500时，该幼树移植成活的棵数是1356，所以“移植成活”的概率是0.904；②随着移植棵数的增加，“移植成活”的频率总在0.880附近摆动，显示出一定的稳定性，可以估计这种幼树“移植成活”的概率是0.880；③若这种幼树“移植成活”的频率的平均值是0.875，则“移植成活”的概率是0.875.其中合理的是（ ）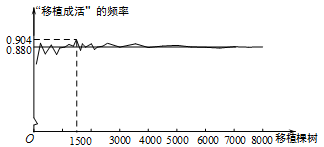
A、①③ B、②③ C、① D、②7. 甲、乙两位同学在一次实验中统计了某一结果出现的频率，给出的统计图如图所示，则符合这一结果的实验可能是（ ）
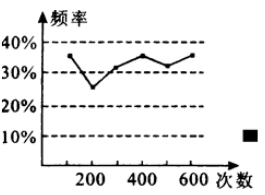A、掷一枚正六面体的骰子，出现5点的概率 B、掷一枚硬币，出现正面朝上的概率 C、任意写出一个整数，能被2整除的概率 D、一个袋子中装着只有颜色不同，其他都相同的 两个红球和一个黄球，从中任意取出一个是黄球的概率8. 一个口袋中有红球、白球共10个，这些球除颜色外都相同，将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有71次摸到红球．请你估计这个口袋中白球的数量为（ ）个．A、29 B、30 C、3 D、79. 在一个不透明的布袋中装有红色、白色玻璃球共20个，除颜色外其他完全相同，小明通过多次摸球试验后发现，其中摸到红色球的频率稳定在15%左右，则口袋中红色球可能有（ ）A、3个 B、5个 C、15个 D、17个10. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
则符合这一结果的实验最有可能的是（ ）
A、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是梅花 B、抛一枚硬币，出现反面的概率 C、袋子里有除了颜色都一样3个红球，2个白球,随机摸一个球是白球的概率 D、抛一个质地均匀的正六面体骰子，向上的面点数大于4二、填空题
-
11. 如图，显示的是用计算机模拟随机投掷一枚图钉的某次试验的结果.小明根据试验结果推断：随着重复试验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，就可以估计“钉尖向上”的概率是0.618.你认为小明的推断是（填写“正确”或“错误”）的.
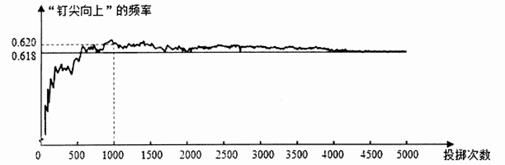12. 在某次数学竞赛中，某校表现突出，成绩均不低于60分.为了更好地了解某校的成绩分布情况，随机抽取利了其中50名学生的成绩（成绩x取整数，总分100分）作为样本进行了整理，结果如表：按规定，成绩在80分以上（包括80分）的选手进入决赛.根据所给信息，请估计该校参赛选手入选决赛的概率为.
13. “阳光体育”活动在我市各校蓬勃开展，某校在一次大课间活动中抽查了10名学生每分钟跳绳次数，获得如下数据（单位：次）：83、89、93、99、117、121、130、146、158、188．其中跳绳次数大于100的频率是；14. 某水果公司以2.2元/千克的成本价购进 苹果.公司想知道苹果的损坏率，从所有苹果中随机抽取若干进行统计，部分数据如下：苹果损坏的频率
0.106
0.097
0.102
0.098
0.099
0.101
估计这批苹果损坏的概率为精确到0.1），据此，若公司希望这批苹果能获得利润23000元，则销售时（去掉损坏的苹果）售价应至少定为元/千克.
15. 如图，这是一幅长为3m，宽为2m的长方形世界杯宣传画，为测量宣传画上世界杯图案的面积，现将宣传画平铺在地上，向长方形宣传画内随机投掷骰子（假设骰子落在长方形内的每一点都是等可能的），经过大量重复投掷试验，发现骰子落在世界杯图案中的频率稳定在常数0.4附近，由此可估计宣传画上世界杯图案的面积约为m2 ．
三、解答题
-
16. 某人承包了一池塘养鱼，他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼，把每条鱼都作上标记，放回鱼塘；过了2天，他让他父亲从鱼塘内打捞上了50条鱼，结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤，平均每条鱼估计2.3斤，你能帮助他估计一下今年的收入情况吗?
17. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共5个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：(1)、请估计：当n很大时，摸到白球的频率将会接近；（精确到0.1）(2)、假如你摸一次，求你摸到白球的概率P；(3)、如果不放回的连续摸两个球，求都摸到白球的概率．（要求画树状图）N摸球的次数
100
200
300
500
800
1000
3000
M摸到白球的次数
65
124
178
302
481
599
1803
m/n摸到白球的概率
0.65
0.62
0.593
0.604
0.601
0.599
0.601
18. 如图，有一个转盘被分成6个相等的扇形，颜色分为红、绿、黄三种，指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时，重新转动).下列事件：①指针指向红色；②指针指向绿色；(③指针指向黄色；④指针不指向黄色，估计各事件的可能性大小，完成下列问题.
(1)、④事件发生的可能性大小是；(2)、多次实验，指针指向绿色的频率的估计值是；(3)、将这些事件的序号按发生的可能性从小到大的顺序排列为： .