河南省信阳市2020年数学中考模拟试卷(5月)
试卷更新日期:2020-07-24 类型:中考模拟
一、选择题
-
1. 在实数0,﹣ ,π,|﹣1|中,最小的数是( )A、0. B、﹣ C、π D、|﹣1|2. 截止到4月21日0时,国外感染新型冠状病毒肺炎的人数已经突破2570000人,“山川异域,风月同天”,携手抗“疫“,刻不容缓.将2570000用科学记数法表示为( )A、2.57×106 B、2.57×105 C、25.7×105 D、2.57×1073. 如图所示为某一物体的主视图,下面是这个物体的是( )
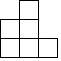 A、
A、 B、
B、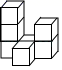 C、
C、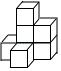 D、
D、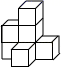 4. 下列运算正确的是( )A、a2÷a8=a﹣4 B、a•a2=a2 C、(a3)2=a6 D、 ﹣ =25. 已知直线 ,将一块含 角的直角三角板 按如图所示方式放置,若 ,则 等于( )
4. 下列运算正确的是( )A、a2÷a8=a﹣4 B、a•a2=a2 C、(a3)2=a6 D、 ﹣ =25. 已知直线 ,将一块含 角的直角三角板 按如图所示方式放置,若 ,则 等于( )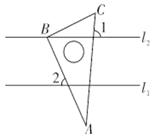 A、 B、 C、 D、6. 某校艺术社团有80名成员,如表是艺术社团成员的年龄分布统计表:对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A、 B、 C、 D、6. 某校艺术社团有80名成员,如表是艺术社团成员的年龄分布统计表:对于不同的x,下列关于年龄的统计量不会发生改变的是( )年龄(单位:岁)
13
14
15
16
17
频数(单位:名)
13
28
x
24﹣x
15
A、平均数、中位数 B、平均数、方差 C、众数、中位数 D、众数、方差7. 关于 的一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定8. 如图,▱ABCD中,CD=4,BC=6,按以下步骤作图:①以点C为圆心,适当长度为半径作弧,分别交BC,CD于M,N两点:②分别以点M,N为圆心,以大于 MN的长为半径画弧,两弧在▱ABCD的内部交于点P;③连接CP并延长交AD于点E,交BA的延长线于点F,则AF的长为( ) A、1 B、2 C、2.5 D、39. 在4张相同的小纸条上分别写上数字﹣2、0、1、2,做成4支签,放在一个盒子中,搅匀后从中任意抽出1支签(不放回),再从余下的3支签中任意抽出1支签,则2次抽出的签上的数字的和为正数的概率为( )A、 B、 C、 D、10. 如图所示,矩形 的两边 、 分别在x轴、y轴上,点C与原点重合,点A的坐标为(-1,2),将矩形 沿x轴向右翻滚,经过第1次翻滚点A对应点记为 ,经过第2次翻滚点 对应点记为 ……依此类推,经过第5次翻滚后点A对应点记为 的坐标为( )
A、1 B、2 C、2.5 D、39. 在4张相同的小纸条上分别写上数字﹣2、0、1、2,做成4支签,放在一个盒子中,搅匀后从中任意抽出1支签(不放回),再从余下的3支签中任意抽出1支签,则2次抽出的签上的数字的和为正数的概率为( )A、 B、 C、 D、10. 如图所示,矩形 的两边 、 分别在x轴、y轴上,点C与原点重合,点A的坐标为(-1,2),将矩形 沿x轴向右翻滚,经过第1次翻滚点A对应点记为 ,经过第2次翻滚点 对应点记为 ……依此类推,经过第5次翻滚后点A对应点记为 的坐标为( ) A、(5,2) B、(6,0) C、(8,1) D、(8,0)
A、(5,2) B、(6,0) C、(8,1) D、(8,0)二、填空题
-
11. 计算: -(- )=.12. 不等式组 的解集是.13. 如图,已知反比例函数y= (k<0)的图象经过Rt△OAB斜边OA的中点D(﹣6,a),且与直角边AB相交于点C.若△AOC的面积为18,则k的值为.
 14. 如图,将半径为4,圆心角为120°的扇形AOB绕B点顺时针旋转60°,点O、A的对应点分别为点O'、A'且点O刚好在弧AB上,则阴影部分的面积为.
14. 如图,将半径为4,圆心角为120°的扇形AOB绕B点顺时针旋转60°,点O、A的对应点分别为点O'、A'且点O刚好在弧AB上,则阴影部分的面积为. 15. 如图,四边形ABCD是边长为m的正方形,若AF= m,E为AB上一点且BE=3,把△AEF沿着EF折叠,得到△A'EF,若△BA'E为直角三角形,则m的值为.
15. 如图,四边形ABCD是边长为m的正方形,若AF= m,E为AB上一点且BE=3,把△AEF沿着EF折叠,得到△A'EF,若△BA'E为直角三角形,则m的值为.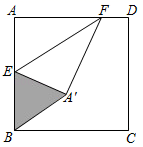
三、解答题
-
16. 先化简,再求值:( ﹣1)÷ ,其中x=tan30°.17. 某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程: .绘画; .唱歌; .跳舞; .演讲; .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.

请结合统计图中的信息解决下列问题:
(1)、这次抽查的学生人数是多少人?(2)、将条形统计图补充完整.(3)、求扇形统计图中课程 所对应扇形的圆心角的度数.(4)、如果该校共有1200名学生,请你估计该校选择课程 的学生约有多少人.18. 如图,在△ABC中,AB=AC,BC是经过⊙H的圆心,交⊙H于点D、E,AB、AC是圆的切线,F、G是切点. (1)、求证:BH=CH;(2)、填空:①当∠FHG=时,四边形FHCG是平行四边形;
(1)、求证:BH=CH;(2)、填空:①当∠FHG=时,四边形FHCG是平行四边形;②当∠FED=时,四边形AFHG是正方形.
19. 如图,渔船跟踪鱼群由西向东航行,到达A处时,测得小岛C位于它的北偏东53°方向,再航行 后达到B处( ),测得小岛C位于它的北偏东45°方向.小岛C的周围 内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?(参考数据: , , )
 20. 随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽气车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元.(1)、求A、B两种型号的汽车每辆进价分别为多少方元?(2)、若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案21. 如图,直线y=ax+2与x轴、y轴分别相交于A,B两点,与双曲线y= (x>0)相交于点P,PC⊥x轴于点C,且PC=4,点A的坐标为(﹣4,0).
20. 随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽气车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元.(1)、求A、B两种型号的汽车每辆进价分别为多少方元?(2)、若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案21. 如图,直线y=ax+2与x轴、y轴分别相交于A,B两点,与双曲线y= (x>0)相交于点P,PC⊥x轴于点C,且PC=4,点A的坐标为(﹣4,0). (1)、求双曲线的解析式;(2)、若点Q为双曲线上点P右侧的一点,过点Q作QH⊥x轴于点H,当以点Q,C,H为顶点的三角形与△AOB相似时,求点Q的坐标.22.
(1)、求双曲线的解析式;(2)、若点Q为双曲线上点P右侧的一点,过点Q作QH⊥x轴于点H,当以点Q,C,H为顶点的三角形与△AOB相似时,求点Q的坐标.22. (1)、问题发现:如图1,在平面直角坐标系中,A点的坐标为(2 ,0),点B的坐标为(0,2),连接AB,点C是AB的中点,点Q是线段AO上的动点,连接OC、CQ,以BQ为边构造等边△BPQ,连接OP、PQ.填空:
(1)、问题发现:如图1,在平面直角坐标系中,A点的坐标为(2 ,0),点B的坐标为(0,2),连接AB,点C是AB的中点,点Q是线段AO上的动点,连接OC、CQ,以BQ为边构造等边△BPQ,连接OP、PQ.填空:①OP与CQ的大小关系是.
②OP的最小值为.
(2)、解决问题:在(1)的条件下,点Q运动的过程中当△ACQ为直角三角形时,求OP的长?(3)、拓展探究:如图2,当点B为直线x=﹣1上一动点,点A(2 ,0),连接AB,以AB为一边向下作等边△ABP,连接OP,请直接写出OP的最小值.23. 如图,抛物线y=ax2+bx+c经过A(﹣1,0)、C(0,3)、B(2,3) (1)、求抛物线的解析式;(2)、线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;(3)、抛物线的对称轴上是否存在点M,使△ABM为直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由(4个坐标).
(1)、求抛物线的解析式;(2)、线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;(3)、抛物线的对称轴上是否存在点M,使△ABM为直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由(4个坐标).