海南省2020年数学中考模拟试卷(二)
试卷更新日期:2020-07-24 类型:中考模拟
一、选择题
-
1. 如果收入2020元记作+2020元,那么支出2020元记作( )A、2020 B、-2020 C、+2020 D、-20102. 若 ,则代数式 的值是( )A、-3 B、-2 C、-1 D、13. 下列计算正确的是( )A、 B、 C、 D、4. 在图所示的4个图案中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 分式方程 的解是( )A、 B、 C、 D、6. 被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积相当于35个标准足球场的总面积.已知每个标准足球场的面积为 ,则FAST的反射面积总面积约为( )A、 B、 C、 D、7. 以平行四边形ABCD的顶点A为原点,直线AD为x轴建立直角坐标系,已知B、D点的坐标分别为(1,3),(4,0),把平行四边形向上平移2个单位,那么C点平移后相应的点的坐标是( )
5. 分式方程 的解是( )A、 B、 C、 D、6. 被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积相当于35个标准足球场的总面积.已知每个标准足球场的面积为 ,则FAST的反射面积总面积约为( )A、 B、 C、 D、7. 以平行四边形ABCD的顶点A为原点,直线AD为x轴建立直角坐标系,已知B、D点的坐标分别为(1,3),(4,0),把平行四边形向上平移2个单位,那么C点平移后相应的点的坐标是( ) A、(3,3) B、(5,3) C、(3,5) D、(5,5)8. 一个布袋里装有 个只有颜色不同的球,其中 个红球, 个白球.从布袋里摸出 个球,记下颜色后放回,搅匀,再摸出 个球,则两次摸到的球都是红球的概率是( )A、 B、 C、 D、9. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、10. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )。
A、(3,3) B、(5,3) C、(3,5) D、(5,5)8. 一个布袋里装有 个只有颜色不同的球,其中 个红球, 个白球.从布袋里摸出 个球,记下颜色后放回,搅匀,再摸出 个球,则两次摸到的球都是红球的概率是( )A、 B、 C、 D、9. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、10. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )。 A、45° B、60° C、75° D、85°11. 如图所示, 是 的直径, 切 于点 ,线段 交 于点 ,连接 ,若 ,则 等于( ).
A、45° B、60° C、75° D、85°11. 如图所示, 是 的直径, 切 于点 ,线段 交 于点 ,连接 ,若 ,则 等于( ). A、27° B、32° C、36° D、54°12. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 , , ,则正方形ADOF的边长是( )
A、27° B、32° C、36° D、54°12. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 , , ,则正方形ADOF的边长是( )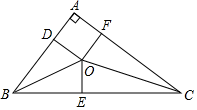 A、 B、2 C、 D、4
A、 B、2 C、 D、4二、填空题
-
13. 因式分解: =.14. 一个正多边形的每个外角为60°,那么这个正多边形的内角和是。15. 如图,在边长为4的等边 中,D,E分别为 , 的中点, 于点F,G为 的中点,连接 ,则 的长为.
 16. 如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2 ,则线段CD的长是.
16. 如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2 ,则线段CD的长是.
三、解答题
-
17.(1)、计算:(2)、解不等式组18. 某市大力发展农村旅游事业,全力打造“凤翔湿地公园”,其中某村的“花海、涂鸦、美食”特色游文化吸引不少人,去年一名村民抓住机遇,返乡创业,投入 万元创办农家乐(餐饮+住宿),一年时间就收回投资的 ,其中餐饮利润是住宿利润的 倍还多 万元,求去年该农家乐餐饮和住宿的利润各为多少万元?19. 某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
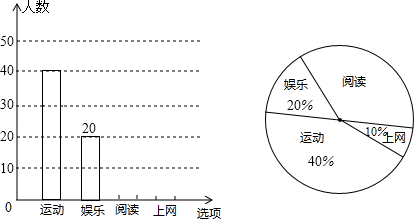 (1)、在这次调查中,一共调查了名学生;(2)、补全条形统计图;(3)、若该校共有1500名学生,估计爱好运动的学生有人;(4)、在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是.20. 如图,为了测得某建筑物的高度 ,在C处用高为 米的测角仪 ,测得该建筑物顶端A的仰角为 ,再向建筑物方向前进40米,又测得该建筑物顶端A的仰角为60°.
(1)、在这次调查中,一共调查了名学生;(2)、补全条形统计图;(3)、若该校共有1500名学生,估计爱好运动的学生有人;(4)、在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是.20. 如图,为了测得某建筑物的高度 ,在C处用高为 米的测角仪 ,测得该建筑物顶端A的仰角为 ,再向建筑物方向前进40米,又测得该建筑物顶端A的仰角为60°. (1)、填空: , ;(2)、求该建筑物的高度 .(结果保留根号)21. 如图 ,在正方形 中, 平分 ,交 于点 ,过点 作 ,交 的延长线于点 ,交 的延长线于点 ,
(1)、填空: , ;(2)、求该建筑物的高度 .(结果保留根号)21. 如图 ,在正方形 中, 平分 ,交 于点 ,过点 作 ,交 的延长线于点 ,交 的延长线于点 , (1)、求证: ;(2)、如图 ,连接 、 ,求证 平分 ;(3)、如图 ,连接 交 于点M, 求 的值。22. 如图,在平面直角坐标系 中,已知抛物线 与直线 都经过 、 两点,该抛物线的顶点为C .
(1)、求证: ;(2)、如图 ,连接 、 ,求证 平分 ;(3)、如图 ,连接 交 于点M, 求 的值。22. 如图,在平面直角坐标系 中,已知抛物线 与直线 都经过 、 两点,该抛物线的顶点为C .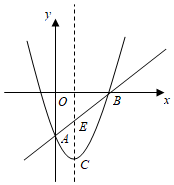 (1)、求此抛物线和直线 的解析式;(2)、设直线 与该抛物线的对称轴交于点E , 在射线 上是否存在一点M , 过M作x轴的垂线交抛物线于点N , 使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;(3)、设点P是直线 下方抛物线上的一动点,当 面积最大时,求点P的坐标,并求 面积的最大值.
(1)、求此抛物线和直线 的解析式;(2)、设直线 与该抛物线的对称轴交于点E , 在射线 上是否存在一点M , 过M作x轴的垂线交抛物线于点N , 使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;(3)、设点P是直线 下方抛物线上的一动点,当 面积最大时,求点P的坐标,并求 面积的最大值.