贵州省遵义市红花岗区2020年数学中考一模试卷
试卷更新日期:2020-07-24 类型:中考模拟
一、选择题
-
1. 在0,﹣2,5,﹣0.3中,绝对值最小的是( )A、0 B、﹣2 C、5 D、﹣0.32. 下列四幅图案,在设计中用到了中心对称的图形是( )A、
 B、
B、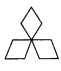 C、
C、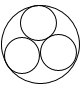 D、
D、 3. 遵义市远期城市化目标是总人口突破500万人,成为特大城市.将500万用科学记数法可表示为( )A、5×108 B、5×107 C、5×106 D、50×1054. 如图,直线AB∥CD,∠A=25°,∠C=45°,则∠P的度数为( )
3. 遵义市远期城市化目标是总人口突破500万人,成为特大城市.将500万用科学记数法可表示为( )A、5×108 B、5×107 C、5×106 D、50×1054. 如图,直线AB∥CD,∠A=25°,∠C=45°,则∠P的度数为( ) A、25° B、45° C、20° D、15°5. 下列运算正确的是( )A、4a﹣a=3 B、a2•a2=a4 C、a3+a2=a5 D、(a2)3=a56. 今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )A、平均数是15 B、众数是10 C、中位数是17 D、方差是7. 2019年由于生猪产量下滑,导致猪肉价格节节攀升,我市在8月份为32元/公斤,到10月份时就已涨到64元/公斤,假设这两个月猪肉价格的平均上涨率相同,求这两次猪肉价格的平均上涨率.设这两月的猪肉价格的平均上涨率为x,则可列方程为( )A、 32(1+x)2=64 B、32x=64 C、64(1﹣x)2=32 D、32+32(1+x)=648. 矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,若OE:ED=1:3.AE= ,则BD=( )
A、25° B、45° C、20° D、15°5. 下列运算正确的是( )A、4a﹣a=3 B、a2•a2=a4 C、a3+a2=a5 D、(a2)3=a56. 今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )A、平均数是15 B、众数是10 C、中位数是17 D、方差是7. 2019年由于生猪产量下滑,导致猪肉价格节节攀升,我市在8月份为32元/公斤,到10月份时就已涨到64元/公斤,假设这两个月猪肉价格的平均上涨率相同,求这两次猪肉价格的平均上涨率.设这两月的猪肉价格的平均上涨率为x,则可列方程为( )A、 32(1+x)2=64 B、32x=64 C、64(1﹣x)2=32 D、32+32(1+x)=648. 矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,若OE:ED=1:3.AE= ,则BD=( ) A、 B、 C、4 D、29. 若一元二次方程x2﹣2x+m=0有两个不相同的实数根,则实数m的取值范围是( )A、m≥1 B、m≤1 C、m>1 D、m<110. 如图,一次函数 与二次函数 交于 和 两点,则当 时x的取值范围是( )
A、 B、 C、4 D、29. 若一元二次方程x2﹣2x+m=0有两个不相同的实数根,则实数m的取值范围是( )A、m≥1 B、m≤1 C、m>1 D、m<110. 如图,一次函数 与二次函数 交于 和 两点,则当 时x的取值范围是( )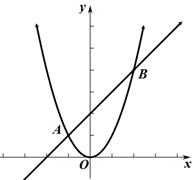 A、 B、 C、 D、 或11. 如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )
A、 B、 C、 D、 或11. 如图所示,矩形纸片ABCD中,AD=6cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )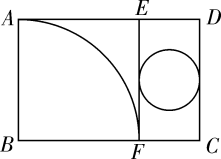 A、3.5cm B、4cm C、4.5cm D、5cm12. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
A、3.5cm B、4cm C、4.5cm D、5cm12. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 计算 .14. 分解因式: = .15. 如图,AB是⊙O的弦,AB长为4,P是⊙O上一个动点(不与A、B重合).过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为.
 16. 如图,在平面直角坐标系中,矩形 的顶点A,D分别在x轴、y轴上,对角线 轴,反比例函数 的图象经过矩形对角线的交点E,若点 , ,则k的值为.
16. 如图,在平面直角坐标系中,矩形 的顶点A,D分别在x轴、y轴上,对角线 轴,反比例函数 的图象经过矩形对角线的交点E,若点 , ,则k的值为.
三、解答题
-
17.(1)、计算: ;(2)、解方程:18. 先化简,再求值: ,其中x为整数且满足不等式组 .19. 为缓解交通压力,建设美丽遵义,市政府加快了风新快线的建设.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=8千米,∠A=45°,∠B=30°.
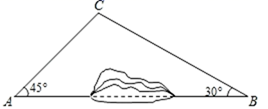 (1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据: ≈1.414, ≈1.732)20. 如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此九(2)班数学兴趣小组对本班同学天饮用饮品的情况进行了调查,发现大致可分为四种:A非碳酸饮料,B瓶装矿泉水,C碳酸饮料,D白开水.
(1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据: ≈1.414, ≈1.732)20. 如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此九(2)班数学兴趣小组对本班同学天饮用饮品的情况进行了调查,发现大致可分为四种:A非碳酸饮料,B瓶装矿泉水,C碳酸饮料,D白开水.根据统计结果绘制如下两个统计图,根据统计图提供的信息解答下列问题:
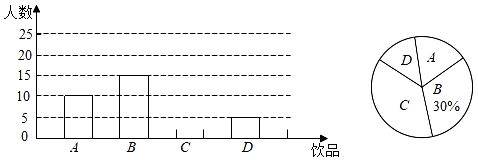 (1)、九(2)班级有多少名同学?并补全条形统计图;(2)、若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如表),则该班同学每天用于饮品的人均花费是多少元?
(1)、九(2)班级有多少名同学?并补全条形统计图;(2)、若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如表),则该班同学每天用于饮品的人均花费是多少元?饮品名称
白开水
瓶装矿泉水
碳酸饮料
非碳酸饮料
平均价格(元/瓶)
0
2
3
4
(3)、为了养成良好的生活习惯,班主任决定在饮用白开水的5名同学(其中有两位班长记为a,b,其余三位记为c,d,e)中随机抽取2名作良好习惯监督员,请用列表法或画树状图的方法,求出抽到的2名同学都不是班长的概率.21. 如图,点O是边长为4的等边三角形ABC的中心,∠EOF的两边与△ABC的边AB,BC分别交于E、F,∠EOF=120°. (1)、如图①,当E为AB中点时,求∠EOF与△ABC的边所围成的四边形OEBF的面积;(2)、如图②,∠EOF绕点O旋转.在旋转过程中四边形OEBF的面积会改变吗?请说明理由.22. 有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?(2)、某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.23. 如图,AC为⊙O的直径,B为AC延长线上一点,且∠BAD=∠ABD=30°,BC=1,AD为⊙O的弦,连结BD,连结DO并延长交⊙O于点E,连结BE交⊙O于点M.
(1)、如图①,当E为AB中点时,求∠EOF与△ABC的边所围成的四边形OEBF的面积;(2)、如图②,∠EOF绕点O旋转.在旋转过程中四边形OEBF的面积会改变吗?请说明理由.22. 有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?(2)、某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.23. 如图,AC为⊙O的直径,B为AC延长线上一点,且∠BAD=∠ABD=30°,BC=1,AD为⊙O的弦,连结BD,连结DO并延长交⊙O于点E,连结BE交⊙O于点M. (1)、求证:直线BD是⊙O的切线;(2)、求⊙O的半径OD的长;(3)、求线段BM的长.24. 如图,抛物线y=x2+bx+c与x轴的交点为A(﹣1,0),B(3,0),与y轴交于点N,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接CP、DP,过点P作CP的垂线与y轴交于点E.
(1)、求证:直线BD是⊙O的切线;(2)、求⊙O的半径OD的长;(3)、求线段BM的长.24. 如图,抛物线y=x2+bx+c与x轴的交点为A(﹣1,0),B(3,0),与y轴交于点N,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接CP、DP,过点P作CP的垂线与y轴交于点E. (1)、求该抛物线的函数关系表达式;(2)、当CP+DP的值最小时,求E点的坐标;(3)、在第四象限的抛物线上任取一点M,连接MN、MB,是否存在点M使得△MNB为直角三角形;若存在,求出此时点M的坐标;若不存在,请说明理由.
(1)、求该抛物线的函数关系表达式;(2)、当CP+DP的值最小时,求E点的坐标;(3)、在第四象限的抛物线上任取一点M,连接MN、MB,是否存在点M使得△MNB为直角三角形;若存在,求出此时点M的坐标;若不存在,请说明理由.