广西岑溪市2020年数学中考一模试卷

试卷更新日期：2020-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. -2020的相反数是（）

A、2020 B、-2020 C、 $\frac{1}{2020}$ D、－ $\frac{1}{2020}$

查看试题解析
2. 下面四个手机应用图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 习近平总书记提出精准扶贫战略以来，各地积极推进精准扶贫，加大帮扶力度，全国脱贫人口数不断增加，脱贫人口接近 $11000000$ 人，将数据 $11000000$ 用科学记数法表示为（）

A、 $1.1 \times 10^{6}$ B、 $1.1 \times 10^{7}$ C、 $1.1 \times 10^{8}$ D、 $1.1 \times 10^{9}$

查看试题解析
4. 如图，平行四边形ABCD中，AE平分 $∠ D A B$ ， $A B = 7$ ， $B C = 4$ ，则CE等于 $($ $)$

A、6 B、5 C、4 D、3

查看试题解析
5. 下列运算正确的是（）

A、 $2 a + 3 a = 5 a {}^{2}$ B、 ${(a + 2 b)}^{2} = a^{2} + 4 b^{2}$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 ${(- a b^{2})}^{3} = - a^{3} b^{6}$

查看试题解析
6. 实数 $a ， b$ 在数轴上的位置如图所示，以下说法正确的是（）

A、 $a + b = 0$ B、 $b < 0$ C、 $a b > 0$ D、 $| b | < | a |$

查看试题解析
7. 计算 $\frac{x - 1}{x^{2} - 1} + \frac{x}{x + 1}$ 的结果为（）

A、-1 B、1 C、 $\frac{1}{x + 1}$ D、 $\frac{1}{x - 1}$

查看试题解析
8. 疫情无情人有情，爱心捐款传真情.疫情期间，某企业员工积极参加献爱心活动，该企业率先捐款的50名员工的捐款情况统计如下表：

金额/元

50

100

200

500

100

人数

6

17

14

8

5

则他们捐款金额的平均数、中位数、众数分别是（）

A、276，100，200 B、276，200，100 C、370，100，100 D、370，200，100

查看试题解析
9. 如图，将 $△ A B C$ 绕点 $C$ 顺时针旋转35°，得 $△ A' B' C$ ，若 $A C ⊥ A' B'$ ，则 $∠ B A C =$ （）

A、65° B、75° C、55° D、35°

查看试题解析
10. 下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图中有3张黑色正方形纸片，第②个图中有5张黑色正方形纸片，第③个图中有7张黑色正方形纸片，…，按此规律排列下去第⑥个图中黑色正方形纸片的张数为（）

A、11 B、13 C、15 D、17

查看试题解析
11. 《九章算术》是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响，该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元，问有多少人？该物品价几何？设有x人，物品价值y元，则所列方程组正确的是（）

A、 ${\begin{matrix} 8 y + 3 = x \\ 7 y - 4 = x \end{matrix}$ B、 ${\begin{matrix} 8 x + 3 = y \\ 7 x - 4 = y \end{matrix}$ C、 ${\begin{matrix} 8 x - 3 = y \\ 7 x + 4 = y \end{matrix}$ D、 ${\begin{matrix} 8 y - 3 = x \\ 7 y + 4 = x \end{matrix}$

查看试题解析
12. 如图，在菱形 $A B C D$ 中，已知 $A B = 4$ ， $∠ A B C = 60^{\circ}$ ， $∠ E A F = 60^{\circ}$ ，点 $E$ 在 $C B$ 的延长线上，点 $F$ 在 $D C$ 的延长线上，有下列结论：① $B E = C F$ ；② $∠ E A B = ∠ C E F$ ；③ $Δ A B E \sim Δ E F C$ ；④若 $∠ B A E = 15^{\circ}$ ，则点 $F$ 到 $B C$ 的距离为 $2 \sqrt{3} - 2$ .则其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 分解因式： $a b^{2} - 2 a b =$

查看试题解析
14. 若式子 $\frac{\sqrt{x + 1}}{2}$ 有意义，则x的取值范围是

查看试题解析
15. 如图，AB为⊙O的直径，半径OA的垂直平分线交⊙O于点C，D，P为优弧AC上一点，则∠APC=°.

查看试题解析
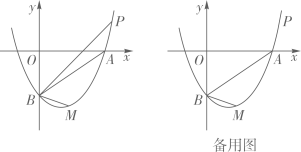
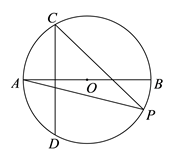16. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象如图所示，对称轴为直线 $x = - 1$ ，则 $y > 3$ 时，该函数的自变量 $x$ 的取值范围是

查看试题解析
17. 如图，矩形ABCD中，AD=4，AB=2 $\sqrt{3}$ ，以点A为圆心，AD为半径画弧交BC于点E，所得的扇形的弧长为.

查看试题解析
18. 如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（2，0），直线y＝ $\frac{\sqrt{3}}{3}$ x+ $\sqrt{3}$ 与⊙O交于B、C两点，则弦BC的长为.

查看试题解析

三、解答题

19. 计算： $\sqrt{8} + | - 3 | - 4 \sin 45 °$

查看试题解析
20. 解不等式组： ${\begin{array}{l} 3 x + 1 > 2 x \\ \frac{x + 5}{4} - \frac{x}{2} \geq \frac{1}{2} \end{array}$ ，把解集在数轴上表示出来.

查看试题解析
21. 为调查某市市民上班时最常用的交通工具的情况，随机抽取了部分市民进行调查，要求被调查者从“A：自行车，B：家庭汽车，C：公交车，D：电动车，E：其他”五个选项中选择最常用的一项，将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图，请结合统计图回答下列问题：

(1)、本次调查中，一共调查了名市民；扇形统计图中，A项对应的扇形圆心角是 °；

(2)、补全条形统计图；

(3)、若甲、乙两人上班时从 $A 、 B 、 C 、 D$ 四种交通工具中随机选择一种，请用列表法或画树状图的方法，求出甲、乙两人恰好选择同一种交通工具上班的概率

查看试题解析
22. 如图，在矩形ABCD中，E是边BC上的点，AE=BC， DF⊥AE，垂足为F，连接DE.
求证：AB=DF.

查看试题解析
23. 如图，为了解水情，制定合适的防洪方案，某防汛部门工作人员乘快艇以每秒10米的速度沿平行于岸边的航道 $A B$ 自西向东航行.在A处测得岸边一建筑物P在北偏东30°方向上，继续航行40秒到达B处，测得建筑物 $P$ 在北偏西60°方向上，求建筑物P到航道 $A B$ 的距离（结果保留根号）.

查看试题解析
24. 为了应对全球新冠肺炎，满足抗疫物资的需求，某电机公司转型生产 $M D$ 呼吸机和 $S M S$ 呼吸机，每台 $M D$ 呼吸机比每台 $S M S$ 呼吸机的生产成本多200元，用5万元生产 $M D$ 呼吸机与用4.5万元生产 $S M S$ 呼吸机的数量相等

(1)、求每台 $M D$ 呼吸机、 $S M S$ 呼吸机的生产成本各是多少元?

(2)、该公司计划生产这两种呼吸机共50台进行试销，其中 $M D$ 呼吸机为 $m$ 台，生产总费用不超过9.8万元，试销时 $M D$ 呼吸机每台售价2500元， $S M S$ 呼吸机每台售价2180元，公司决定从销售 $M D$ 呼吸机的利润中按每台捐献 $a (a < 120)$ 元作为公司捐献国家抗疫的资金，若公司售完50台呼吸机并捐献资金后获得的利润不超过23000元，求 $a$ 的取值范围.

查看试题解析
25. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 60 °$ ，点O为 $A B$ 上一点，且 $3 A O = A B$ ，以 $O A$ 为半径作圆O，交 $A C$ 于点D，交 $A B$ 于点E， $D E$ 与 $O C$ 相交于F.

(1)、求证： $C B$ 与 $⊙ O$ 相切；

(2)、若 $A B = 6$ ，求 $D F$ 的长度.

查看试题解析
26. 若二次函数 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴分别交于点 $A (3 ， 0)$ 、 $B (0 ， - 2)$ ，且过点 $C (2 ， - 2)$ .

(1)、求二次函数表达式；

(2)、若点 $P$ 为抛物线上第一象限内的点，且 $S_{Δ P A B} = 4$ ，求点 $P$ 的坐标；

(3)、在抛物线上（ $A B$ 下方）是否存在点 $M$ ，使 $∠ A B O = ∠ A B M$ ？若存在，求出点 $M$ 到 $y$ 轴的距离；若不存在，请说明理由.

查看试题解析

金额/元	50	100	200	500	100
人数	6	17	14	8	5