广东省惠州市惠城区四校2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-07-24 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示的车标，可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式中，正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $- \sqrt{3^{2}} = - 3$ C、 $\sqrt{{(\pm 3)}^{2}} = \pm 3$ D、 $\sqrt{3^{2}} = \pm 3$

查看试题解析
3. 在下列各数3.1415、 $\sqrt[3]{8}$ 、0.2060060006…、 $\sqrt[3]{9}$ 、 $0. \dot{2}$ 、 $- π$ 、 $\sqrt[3]{5}$ 、 $\frac{22}{7}$ 、 $\sqrt{27}$ 无理数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
4. 若y轴上的点P到x轴的距离为3，则点P的坐标是（）

A、（3，0） B、（0，3） C、（3，0）或（﹣3，0） D、（0，3）或（0，﹣3）

查看试题解析
5. 如图，给出下列条件，①∠1＝∠3；②∠2＝∠4；③∠B＝∠DCE；④∠D＝∠DCE.其中能推出AD∥BC的条件为（）

A、②③④ B、②④ C、②③ D、①④

查看试题解析
6. 在平面直角坐标系中，已知线段AB的两个端点分别是A(- 4 ，-1).B(1，1) 将线段AB平移后得到线段A ’B’，若点A的坐标为 (-2 ， 2 ) ，则点 B’的坐标为（）

A、( 3 ， 4 ) B、( 4 ， 3 ) C、（一l ，一2 ) D、(-2，-1)

查看试题解析
7. 已知x ， y是实数，并且 ${(x + 3)}^{2} + \sqrt{3 - 2 y} = 0$ ，则 $x + 2 y$ 的值是（）

A、 $- \frac{3}{2}$ B、0 C、 $\frac{3}{2}$ D、2

查看试题解析
8. 八块相同的长方形地砖拼成一个长方形，每块长方形地砖的长等于（）

A、 $15 c m$ B、 $30 c m$ C、 $40 c m$ D、 $45 c m$

查看试题解析
9.
如图，AB∥EF，CD⊥EF于点D，若∠ABC=40°，则∠BCD=（　　）

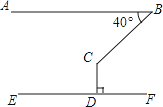A、140° B、130° C、120° D、110°

查看试题解析
10. 有一个数值转换器，原理如下：当输入的 x 为 16 时，输出的 y 是（）

A、 $\sqrt{2}$ B、 $\sqrt{4}$ C、4 D、8

查看试题解析

二、填空题

11. $\sqrt{16}$ 的算术平方根为， $- 27$ 的立方根为

查看试题解析
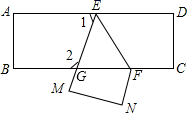
12. 已知方程 $2 x^{a - 5} - (b - 2) y^{| b | - 1} = 4$ 是关于 $x$ ， $y$ 的二元一次方程，则 $a - 2 b$ ＝．

查看试题解析
13. 在明朝程大位《算法统宗》中有首住店诗：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空.诗的大意是：一些客人到李三公的店中住宿，如果每一间客房住7人，那么有7人无房可住；如果每一间客房住9人，那么就空出一间房.设该店有客房x间，房客y人，则可列方程组为.

查看试题解析
14. 如图，把一张长方形纸片ABCD沿EF折叠后，D、C分别在M、N的位置上，EM与BC的交点为G，若∠EFG＝65°，则∠2＝．

查看试题解析
15. 如图，在平面直角坐标系中，从点P₁（﹣1，0），P₂（﹣1，﹣1），P₃（1，﹣1），P₄（1，1），P₅（﹣2，1），P₆（﹣2，﹣2），…依次扩展下去，则P₂₀₂₀的坐标为．

查看试题解析

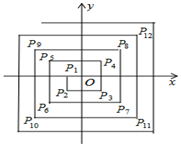
三、解答题

16. 计算：

(1)、 $\sqrt{16} - \sqrt[3]{64} \times \sqrt[3]{- 8}$

(2)、 $\sqrt[3]{- 27} + | 3 - \sqrt{5} | - {(\sqrt{9} - \sqrt[3]{8})}^{2} + 3 \sqrt{5}$

查看试题解析
17. 解方程（组）

(1)、 $2 {(x - 1)}^{2} = 32$

(2)、 ${\begin{array}{l} \frac{x}{2} + \frac{y}{3} = - 2 \\ 3 x - 4 y = 6 \end{array}$

查看试题解析
18. 已知 $2 a - 1$ 的算术平方根是3， $a - b + 2$ 的立方根是2，求 $a - 4 b$ 的平方根．

查看试题解析
19. 已知方程组 ${\begin{array}{l} 2 x + 5 y = - 6 \\ a x - b y = - 4 \end{array}$ 与方程组 ${\begin{array}{l} 3 x - 5 y = 16 \\ b x + a y = - 8 \end{array}$ 的解相同．求 ${(2 a + b)}^{2020}$ 的值．

查看试题解析
20. 如图，已知 $A (- 4 ， - 1)$ ， $B (- 5 ， - 4)$ ， $C (- 1 ， - 3)$ ， $Δ A B C$ 经过平移得到的 $Δ A^{'} B^{'} C^{'}$ ， $Δ A B C$ 中任意一点 $P (x_{1} ， y_{1})$ 平移后的对应点为 $P^{'} (x_{1} + 6 ， y_{1} + 4)$ ．

(1)、请在图中作出 $Δ A^{'} B^{'} C^{'}$ ；

(2)、写出点 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ 的坐标；

(3)、求 $Δ A B C$ 的面积．

查看试题解析
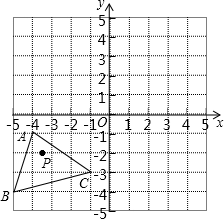21. 如图，点D，F在线段AB上，点E，G分别在线段BC和AC上，CD∥EF，∠1=∠2．

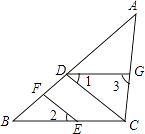(1)、判断DG与BC的位置关系，并说明理由；

(2)、若DG是∠ADC的平分线，∠3=85°，且∠DCE：∠DCG=9：10，试说明AB与CD有怎样的位置关系？

查看试题解析
22. 为了响应市委和市政府“绿色环保，节能减排”的号召，幸福商场用3300元购进甲、乙两种节能灯共计100只，很快售完．这两种节能灯的进价、售价如下表：

进价（元/只）
售价(元/只）
甲种节能灯
30
40
乙种节能灯
35
50

(1)、求幸福商场甲、乙两种节能灯各购进了多少只?

(2)、全部售完100只节能灯后，商场共计获利多少元？

查看试题解析
23. 已知，直线AB∥DC，点P为平面上一点，连接AP与CP．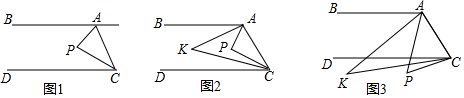

(1)、如图1，点P在直线AB、CD之间，当∠BAP=60°，∠DCP=20°时，求∠APC度数．

(2)、如图2，点P在直线AB、CD之间，∠BAP与∠DCP的角平分线相交于点K，写出∠AKC与∠APC之间的数量关系，并说明理由．

(3)、如图3，点P落在CD外，∠BAP与∠DCP的角平分线相交于点K，∠AKC与∠APC有何数量关系？并说明理由．

查看试题解析

	进价（元/只）	售价(元/只）
甲种节能灯	30	40
乙种节能灯	35	50