广东省深圳市南山区深大附中2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-07-24 类型:期中考试
一、单选题
-
1. 如果分式 有意义,则x的取值范围是( )A、x=﹣3 B、x>﹣3 C、x≠﹣3 D、x<﹣32. 下列图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 不等式 的正整数解的个数有( )A、2 B、3 C、4 D、54. 将下列多项式分解因式,得到的结果不含因式 的是( ).A、 B、 C、 D、5. 已知过一个多边形的一个顶点的所有对角线共有5条,则这个多边形的内角和为( )A、720° B、1080° C、1260° D、1440°6. 若分式方程 有增根,则m等于( )A、-3 B、-2 C、3 D、27. 如图,在▱ABCD中,DE平分∠ADC,AD=8,BE=3,则▱ABCD的周长是( )
3. 不等式 的正整数解的个数有( )A、2 B、3 C、4 D、54. 将下列多项式分解因式,得到的结果不含因式 的是( ).A、 B、 C、 D、5. 已知过一个多边形的一个顶点的所有对角线共有5条,则这个多边形的内角和为( )A、720° B、1080° C、1260° D、1440°6. 若分式方程 有增根,则m等于( )A、-3 B、-2 C、3 D、27. 如图,在▱ABCD中,DE平分∠ADC,AD=8,BE=3,则▱ABCD的周长是( ) A、16 B、14 C、26 D、248. 下列命题正确的个数是( )
A、16 B、14 C、26 D、248. 下列命题正确的个数是( )⑴若x2+kx+25是一个完全平方式,则k的值等于10;(2)正六边形的每个内角都等于相邻外角的2倍;(3)一组对边平行,一组对角相等的四边形是平行四边形;(4)顺次连结四边形的四边中点所得的四边形是平行四边形
A、1 B、2 C、3 D、49. 如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,2),则关于x的不等式x+m<kx﹣1的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、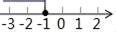 D、
D、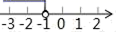 10. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=2,AB=6,则△ABD的面积是( )
10. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=2,AB=6,则△ABD的面积是( ) A、3 B、6 C、12 D、1811. 某商场要销售70件积压衬衫,销售30件后,降低售价,每天能多售出10件,结果70件衬衫一共用5天全部售完,原来每天销售多少件衬衫?设原来每天销售x件衬衫,下面列出的方程正确的是( )A、 B、 C、 D、12. 如图,已知A(3,1)与B(1,0),PQ是直线 上的一条动线段且 (Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )
A、3 B、6 C、12 D、1811. 某商场要销售70件积压衬衫,销售30件后,降低售价,每天能多售出10件,结果70件衬衫一共用5天全部售完,原来每天销售多少件衬衫?设原来每天销售x件衬衫,下面列出的方程正确的是( )A、 B、 C、 D、12. 如图,已知A(3,1)与B(1,0),PQ是直线 上的一条动线段且 (Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )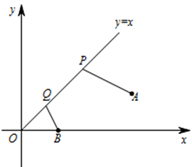 A、( , ) B、( , ) C、(0,0) D、(1,1)
A、( , ) B、( , ) C、(0,0) D、(1,1)二、填空题
-
13. 分解因式: .14. 不等式组 的解集是x>4,那么m的取值范围是 .15. 若△ABC三边分别为a , b , c , 且满足 ,则△ABC的形状是 .16. 如图,在正方形ABCD中,AB=4,点E、F分别在CD、AD上,CE=DF,BE、CF相交于点G,若图中阴影部分的面积与正方形ABCD的面积之比为3:4,则△BCG的面积为 .

三、解答题
-
17. 解不等式组 ,并把解集在数轴上表示出来.18. 先化简: ,然后在 , ,0,1,2中选取一个合适的数代入求值.19. 解分式方程: .20. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
 (1)、画出后将如图所示:△A1B1C1是所求的三角形.
(1)、画出后将如图所示:△A1B1C1是所求的三角形. (2)、画出将△A1B1C1绕点C1按顺时针方向旋转90°后所得到的△A2B2C1 .21. 为迎接全国文明城市的评选,市政府决定对春风路进行市政化改造,经过市场招标,决定聘请甲、乙两个工程队合作施工,已知春风路全长24千米,甲工程队每天施工的长度比乙工程队每天施工长度的多施工0.4千米,由甲工程队单独施工完成任务所需要的天数是乙工程队单独完成任务所需天数的 .(1)、求甲、乙两个工程队每天各施工多少千米?(2)、若甲工程队每天的施工费用为0.8万元,乙工程队每天的施工费用为0.5万元,要使两个工程队施工的总费用不超过7万元,则甲工程队至多施工多少天?22. 如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.
(2)、画出将△A1B1C1绕点C1按顺时针方向旋转90°后所得到的△A2B2C1 .21. 为迎接全国文明城市的评选,市政府决定对春风路进行市政化改造,经过市场招标,决定聘请甲、乙两个工程队合作施工,已知春风路全长24千米,甲工程队每天施工的长度比乙工程队每天施工长度的多施工0.4千米,由甲工程队单独施工完成任务所需要的天数是乙工程队单独完成任务所需天数的 .(1)、求甲、乙两个工程队每天各施工多少千米?(2)、若甲工程队每天的施工费用为0.8万元,乙工程队每天的施工费用为0.5万元,要使两个工程队施工的总费用不超过7万元,则甲工程队至多施工多少天?22. 如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上. (1)、求证:BC=2AB;(2)、若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
(1)、求证:BC=2AB;(2)、若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:①求点F的运动时间t的值;②求线段AG的长度.
23. 如图,在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造平行四边形PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒. (1)、直接写出当点C运动到线段OB的中点时,求t的值及点E的坐标.(2)、当点C在线段OB上运动时,四边形ADEC的面积为S.
(1)、直接写出当点C运动到线段OB的中点时,求t的值及点E的坐标.(2)、当点C在线段OB上运动时,四边形ADEC的面积为S.①求证:四边形ADEC为平行四边形.
②写出s与t的函数关系式,并求出t的取值范围.
(3)、是否存在某一时刻,使OC是PC的一半?若存在,求出t的值,若不存在,请说明理由.