广东省深圳市福田区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-07-24 类型:期中考试
一、单选题
-
1. 下列等式从左到右的变形属于因式分解的是( )A、a2﹣2a+1=(a﹣1)2 B、a(a+1)(a﹣1)=a3﹣a C、6x2y3=2x2•3y3 D、2. 下列不等式变形错误的是( )A、若 a>b,则 1﹣a<1﹣b B、若 a<b,则 ax2≤bx2 C、若 ac>bc,则 a>b D、若 m>n,则 >3. 下列汽车标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
4. 如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )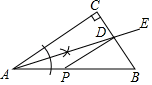 A、2 B、3 C、4 D、无法确定5. 已知a , b , c是△ABC的三条边的长度,且满足a2-b2=c(a-b),则△ABC是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形6. 如果不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、7. 如图,函数 和 的图象相交于A(m,3),则不等式 的解集为( )
A、2 B、3 C、4 D、无法确定5. 已知a , b , c是△ABC的三条边的长度,且满足a2-b2=c(a-b),则△ABC是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形6. 如果不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、7. 如图,函数 和 的图象相交于A(m,3),则不等式 的解集为( )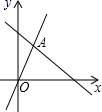 A、 B、 C、 D、8. 如图,在△ABC中,∠A为钝角,AB=20cm,AC=12cm,点P从点B出发以3cm/s的速度向点A运动,点Q同时从点A出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.当△APQ是等腰三角形时,运动的时间是( )
A、 B、 C、 D、8. 如图,在△ABC中,∠A为钝角,AB=20cm,AC=12cm,点P从点B出发以3cm/s的速度向点A运动,点Q同时从点A出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.当△APQ是等腰三角形时,运动的时间是( ) A、2.5s B、3s C、3.5s D、4s9. 如图, 是由 绕点 顺时针旋转 后得到的图形,若点 恰好落在 上,且 的度数为( )
A、2.5s B、3s C、3.5s D、4s9. 如图, 是由 绕点 顺时针旋转 后得到的图形,若点 恰好落在 上,且 的度数为( )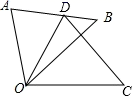 A、 B、 C、 D、10. 已知等边△ABC的边长为8,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,点D是AC边的中点,连接DQ,则DQ的最小值是( )
A、 B、 C、 D、10. 已知等边△ABC的边长为8,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,点D是AC边的中点,连接DQ,则DQ的最小值是( )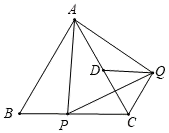 A、 B、4 C、 D、不能确定
A、 B、4 C、 D、不能确定二、填空题
-
11. 把多项式a3b﹣9ab分解因式的结果是 .12. 命题“如a2>b2 , 则a>b”的逆命题是命题(填“真”或“假”).13. 如图,△ABC中,∠ACB=90°,D、E是边AB上两点,且CD垂直平分BE,CE平分∠ACD,若BC=2,则AC的长为.
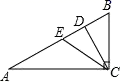 14. 如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有.(填上所有正确结论的序号)
14. 如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有.(填上所有正确结论的序号)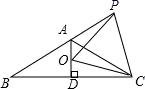
三、解答题
-
15. 新冠肺炎使得湖北的物资紧缺,为支援疫区,某村捐赠蔬菜30吨,水果13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往港口,已知一辆甲种货车可装蔬菜和水果共5吨,且一辆甲种货车可装的蔬菜重量(单位:吨)是其可装的水果重量的4倍,一辆乙种货车可装蔬菜水果各2吨;(1)、一辆甲种货车可装载蔬菜、水果各多少吨?(2)、该村安排甲、乙两种货车时有几种方案?请你帮助设计出来;(3)、若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1500元,则该村应选择哪种方案?使运费最少?最少运费是多少元?16. 如图,直线 与x轴交于点A,与y轴交于点B,与直线 交于点E,点E的横坐标为3.
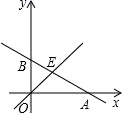 (1)、直接写出b值:;(2)、在y轴上有一点M,使得△ABM是等腰三角形,直接写出所有可能的点M的坐标:;(3)、在x轴上有一点P(m,0),过点P作x轴的垂线,与直线 交于点C,与直线 交于点D,若CD=2OB,求m的值.
(1)、直接写出b值:;(2)、在y轴上有一点M,使得△ABM是等腰三角形,直接写出所有可能的点M的坐标:;(3)、在x轴上有一点P(m,0),过点P作x轴的垂线,与直线 交于点C,与直线 交于点D,若CD=2OB,求m的值.