广东省广州市香浓教育集团2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-07-24 类型:期中考试
一、单选题
-
1. 实数 的值是( )A、 B、8 C、 D、42. 若 在实数范围内有意义,则x的取值范围是( )A、x>0 B、x>3 C、x≥3 D、x≤33. 以下列各组数为边长,能构成直角三角形的是( )A、1,2,3 B、2,3,4 C、2,2,3 D、1,2,4. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、5. 顺次连接任意四边形ABCD各边的中点所得四边形是( )A、一定是平行四边形 B、一定是菱形 C、一定是矩形 D、一定是正方形6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,小正方形的边长为1,连接小正方形的三个顶点可得△ABC,则AB边上的高是( )
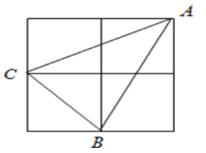 A、 B、 C、 D、8. 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
A、 B、 C、 D、8. 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )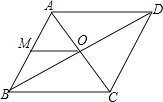 A、5cm B、10cm C、20cm D、40cm9. 如图,把菱形 沿 折叠, 落在 边上的 处,若 ,则 的大小为( )
A、5cm B、10cm C、20cm D、40cm9. 如图,把菱形 沿 折叠, 落在 边上的 处,若 ,则 的大小为( ) A、 B、 C、 D、10. 在矩形纸片ABCD中,AB=6,AD=10.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ . 当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为( )
A、 B、 C、 D、10. 在矩形纸片ABCD中,AB=6,AD=10.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ . 当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为( )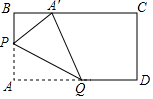 A、8cm B、6cm C、4cm D、2cm
A、8cm B、6cm C、4cm D、2cm二、填空题
-
11. 计算: ﹣ = .12. 如图由于台风的影响,一棵树在离地面 处折断,树顶落在离树干底部 处,则这棵树在折断前的高度是.
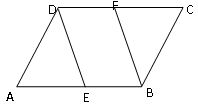
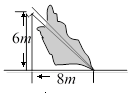 13. 如图,在平行四边形ABCD中,E为AB边上的点,BE=BC,将△ADE沿DE翻折,点A的对应点F恰好落在CE上,∠ADF=84°,则∠BEC=。
13. 如图,在平行四边形ABCD中,E为AB边上的点,BE=BC,将△ADE沿DE翻折,点A的对应点F恰好落在CE上,∠ADF=84°,则∠BEC=。 14. 如图,在 中, ,点 分别在 上,且 ,点 分别为 的中点,则 的长为 .
14. 如图,在 中, ,点 分别在 上,且 ,点 分别为 的中点,则 的长为 .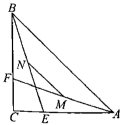 15. 如图,在平面直角坐标系中,等腰Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,3),点C的坐标为(1,0),点P为斜边OB上的一个动点,则PA+PC的最小值为 .
15. 如图,在平面直角坐标系中,等腰Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,3),点C的坐标为(1,0),点P为斜边OB上的一个动点,则PA+PC的最小值为 .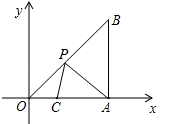
三、解答题
-
16. 已知x= +1,y= -1,求代数式x2-y2的值.17.(1)、(2)、18. 如图,在▱ABCD中,E、F分别是AB、CD的中点,求证:四边形EBFD是平行四边形.
 19. 已知x=2﹣ ,求代数式(7+4 )x2+(2+ )x+ 的值.20. 如图,矩形 的对角线 相交于点 .
19. 已知x=2﹣ ,求代数式(7+4 )x2+(2+ )x+ 的值.20. 如图,矩形 的对角线 相交于点 .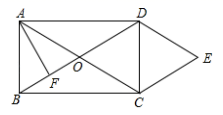 (1)、求证:四边形 为菱形;(2)、 垂直平分线段 于点 ,求 的长.21. 如图所示,在Rt△ABC中,∠BAC=90°,AC=AB,∠DAE=45°,且BD=3,CE=4 ,求DE的长.
(1)、求证:四边形 为菱形;(2)、 垂直平分线段 于点 ,求 的长.21. 如图所示,在Rt△ABC中,∠BAC=90°,AC=AB,∠DAE=45°,且BD=3,CE=4 ,求DE的长.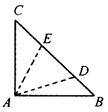 22. 如图,点 是正方形 对角线 上一点, 于 ,点 、 分别是 、 的中点.
22. 如图,点 是正方形 对角线 上一点, 于 ,点 、 分别是 、 的中点.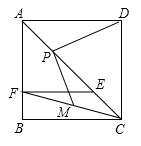 (1)、求证: ;(2)、当点 在对角线 (不含 、 两点)上运动时, 是否为定值?如果是,请求其值;如果不是,试说明理由.23. 在菱形ABCD中,∠BAD=60°
(1)、求证: ;(2)、当点 在对角线 (不含 、 两点)上运动时, 是否为定值?如果是,请求其值;如果不是,试说明理由.23. 在菱形ABCD中,∠BAD=60°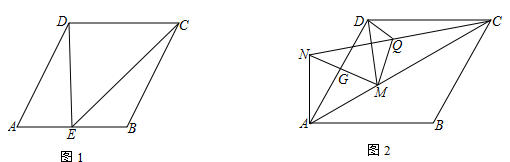 (1)、如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长(2)、如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论(3)、在(2)的条件下,若AC= ,请你直接写出DM+CN的最小值24. 如图1,在平面直角坐标系中,点A(0,4),点B(m , 0),以AB为边在右侧作正方形ABCD .
(1)、如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长(2)、如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论(3)、在(2)的条件下,若AC= ,请你直接写出DM+CN的最小值24. 如图1,在平面直角坐标系中,点A(0,4),点B(m , 0),以AB为边在右侧作正方形ABCD .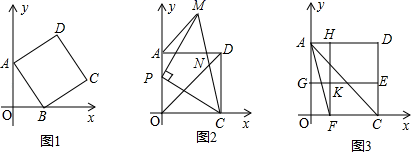 (1)、当点B在x轴正半轴上运动时,求点C点的坐标.(用m表示)(2)、当m=0时,如图2,P为OA上一点,过点P作PM⊥PC , PM=PC , 连MC交OD于点N , 求AM+2DN的值;(3)、如图3,在第(2)问的条件下,E、F分别为CD、CO上的点,作EG∥x轴交AO于G , 作FH∥y轴交AD于H , K是EG与FH的交点.若S四边形KFCE=2S四边形AGKH , 试确定∠EAF的大小,并证明你的结论.
(1)、当点B在x轴正半轴上运动时,求点C点的坐标.(用m表示)(2)、当m=0时,如图2,P为OA上一点,过点P作PM⊥PC , PM=PC , 连MC交OD于点N , 求AM+2DN的值;(3)、如图3,在第(2)问的条件下,E、F分别为CD、CO上的点,作EG∥x轴交AO于G , 作FH∥y轴交AD于H , K是EG与FH的交点.若S四边形KFCE=2S四边形AGKH , 试确定∠EAF的大小,并证明你的结论.