四川省南充市2020年中考数学一模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
1. 下列各数中,属于无理数的是( )A、3.14 B、0.2020... C、 D、2. 下列计算,错误的是( )A、 B、 C、当 时, D、当 时,3. 针对所给图形,如果不区分颜色,说法正确的是( )
 A、是轴对称图形 B、是中心对称图形 C、既是轴对称图形,又是中心对称图形 D、非轴对称图形,也非中心对称图形4. 下列说法正确的是( )A、可能性很大的事件,在一次试验中一定发生 B、可能性很小的事件,在一次试验中可能发生 C、必然事件,在一次试验中有可能不会发生 D、不可能事件,在一次试验中也可能发生5. 若 的一边为4,另两边同时满足方程 ,则 的周长( )A、为10 B、为11 C、为12 D、不确定6. 将抛物线 向左平移1个单位后的解析式为( )A、 B、 C、 D、7. 如图,小王从A处出发沿北偏东 方向行走至B处,又从B处沿南偏东 方向行走至C处,则 等于( )
A、是轴对称图形 B、是中心对称图形 C、既是轴对称图形,又是中心对称图形 D、非轴对称图形,也非中心对称图形4. 下列说法正确的是( )A、可能性很大的事件,在一次试验中一定发生 B、可能性很小的事件,在一次试验中可能发生 C、必然事件,在一次试验中有可能不会发生 D、不可能事件,在一次试验中也可能发生5. 若 的一边为4,另两边同时满足方程 ,则 的周长( )A、为10 B、为11 C、为12 D、不确定6. 将抛物线 向左平移1个单位后的解析式为( )A、 B、 C、 D、7. 如图,小王从A处出发沿北偏东 方向行走至B处,又从B处沿南偏东 方向行走至C处,则 等于( )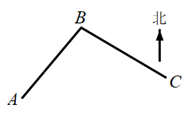 A、 B、 C、 D、8. 不等式组 的最大整数解为a,最小整数解为b,则 ( )A、-14 B、-15 C、-16 D、-179. 如图A,B,C是 上顺次3点,若 , , 分别是 内接正三角形、正方形、正n边形的一边,则 ( )
A、 B、 C、 D、8. 不等式组 的最大整数解为a,最小整数解为b,则 ( )A、-14 B、-15 C、-16 D、-179. 如图A,B,C是 上顺次3点,若 , , 分别是 内接正三角形、正方形、正n边形的一边,则 ( ) A、9 B、10 C、12 D、1510. 如图,正方形 中,点E是 边的中点.将 沿 对折至 ,延长 交 边于点G,连接 , .下列结论:① ;② ;③ ;④ .其中正确的有( )
A、9 B、10 C、12 D、1510. 如图,正方形 中,点E是 边的中点.将 沿 对折至 ,延长 交 边于点G,连接 , .下列结论:① ;② ;③ ;④ .其中正确的有( )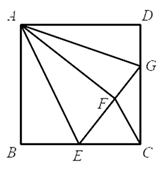 A、①② B、①③④ C、②③④ D、①②③④
A、①② B、①③④ C、②③④ D、①②③④二、填空题
-
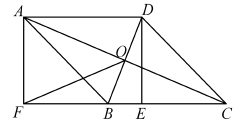
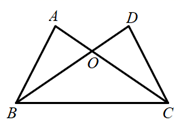
11. 若 ,则 的值是 .12. 以方程组的 ,解为坐标的点 在第象限.13. 下个月学校将为片区学校展示“音乐、体育、美术”兴趣活动观摩,小明、小丽随机从三个场所选择一个担任志愿者服务,两人恰好选择同一场所的概率是.14. 如图, 与 交于O, ,要使 ,可以补充一个边或角的条件是.
 15. 如图, 是 的高, , , ,则 .
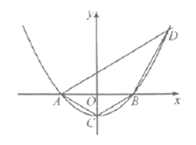
15. 如图, 是 的高, , , ,则 .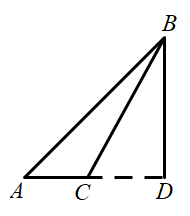 16. 如图,抛物线 经过点 , .若点Q到y轴的距离小于2,则n的取值范围是.
16. 如图,抛物线 经过点 , .若点Q到y轴的距离小于2,则n的取值范围是.
三、解答题
-
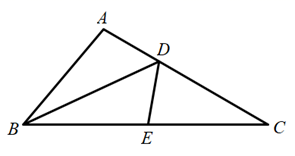
17. 计算: .18. 如图, 是 的角平分线,在 上截取 .若 , ,试求 的度数.
 19. 为了解社区居民公共卫生意识情况,社区网格员随机抽查了若干居民开展“抗击疫情相关规定”有奖问答活动,并用得到的数据绘制了条形统计图.
19. 为了解社区居民公共卫生意识情况,社区网格员随机抽查了若干居民开展“抗击疫情相关规定”有奖问答活动,并用得到的数据绘制了条形统计图.
请根据图中信息,解答下列问题:
(1)、本次抽查的居民人数;(2)、本次抽查获取的样本数据的平均数、众数和中位数;(3)、社区决定对本区500户居民开展这项有奖间答活动(每户抽1人),得10分者设为“一等奖”.请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?20. a为实数,关于x的方程 有两个实数根 , .(1)、求a的取值范围.(2)、若 ,试求a的值.21. 如图,直线 与x轴交于点 ,与 轴交于点 ,将线段 绕点A逆时针旋转 得到线段 ,双曲线 经过点C.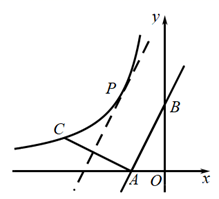 (1)、求直线 和双曲线 的解析式.(2)、平移直线 ,使它与双曲线 有唯一公共点P时,求点P的坐标.22. 如图,AB是⊙O的直径,点C是 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且 ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
(1)、求直线 和双曲线 的解析式.(2)、平移直线 ,使它与双曲线 有唯一公共点P时,求点P的坐标.22. 如图,AB是⊙O的直径,点C是 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且 ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.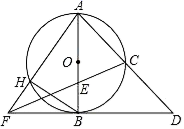 (1)、求证:BD是⊙O的切线;(2)、当OB=2时,求BH的长.23. 某商店经营一款新电动玩具,进货单价是30元。在1个月的试销阶段,售价是40元,销售量是400件.根据市场调查,销售单价若每再涨1元,1个月就会少售出10件.(1)、若商店在1个月获得了6000元销售利润,求这款玩具销售单价是定为多少元的,并考虑了顾客更容易接受.(2)、若玩具生产厂家规定销售单价不低于43元,且商店每月要完成不少于350件的销售任务,求商店销售这款玩具1个月能获得的最大利润.
(1)、求证:BD是⊙O的切线;(2)、当OB=2时,求BH的长.23. 某商店经营一款新电动玩具,进货单价是30元。在1个月的试销阶段,售价是40元,销售量是400件.根据市场调查,销售单价若每再涨1元,1个月就会少售出10件.(1)、若商店在1个月获得了6000元销售利润,求这款玩具销售单价是定为多少元的,并考虑了顾客更容易接受.(2)、若玩具生产厂家规定销售单价不低于43元,且商店每月要完成不少于350件的销售任务,求商店销售这款玩具1个月能获得的最大利润.