四川省乐山市沙湾区2020年中考数学模拟试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
1. 计算: ( )A、-1 B、 C、 D、2. 下列立体图形中,主视图是三角形的是( ).A、
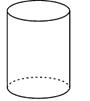 B、
B、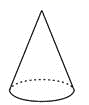 C、
C、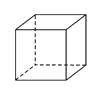 D、
D、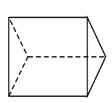 3. 在 中, , ,则 ( )A、 B、
3. 在 中, , ,则 ( )A、 B、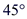 C、
D、
4. 口袋中有白球和红球共10个,这些球除颜色外其它都相同. 小明将口袋中的球搅匀后随机从中摸出一个球,记下颜色后放回口袋中,小明继续重复这一过程,共摸了100次,结果有40次是红球,请你估计口袋中红球的个数是( )A、3 B、4 C、5 D、65. 如图,点A、B、C在⊙ 上, 为等边三角形,则 ( )
C、
D、
4. 口袋中有白球和红球共10个,这些球除颜色外其它都相同. 小明将口袋中的球搅匀后随机从中摸出一个球,记下颜色后放回口袋中,小明继续重复这一过程,共摸了100次,结果有40次是红球,请你估计口袋中红球的个数是( )A、3 B、4 C、5 D、65. 如图,点A、B、C在⊙ 上, 为等边三角形,则 ( )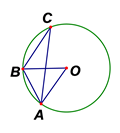 A、 B、 C、 D、6. 二次函数 的图象是一条抛物线,下列关于该抛物线的说法正确的是( )A、开口向上 B、对称轴是 C、当 时,函数的最大值是-1 D、抛物线与 轴有两个交点7. 身高1.6米的小明同学利用相似三角形测量学校旗杆的高度,上午10点,小明在阳光下的影长为1米,此时测得旗杆的影长为9米,则学校旗杆的高度是( )A、 米 B、 米 C、 米 D、 米8. 某服装店一月份营业额为10万元,一季度的营业额共48万元,若平均每月营业额的增长率为x,则根据题意可列方程为( )A、 B、 C、 D、9. 如图,矩形 中, , ,以 为直径的半圆与 相切,连接 . 则阴影部分的面积为( )
A、 B、 C、 D、6. 二次函数 的图象是一条抛物线,下列关于该抛物线的说法正确的是( )A、开口向上 B、对称轴是 C、当 时,函数的最大值是-1 D、抛物线与 轴有两个交点7. 身高1.6米的小明同学利用相似三角形测量学校旗杆的高度,上午10点,小明在阳光下的影长为1米,此时测得旗杆的影长为9米,则学校旗杆的高度是( )A、 米 B、 米 C、 米 D、 米8. 某服装店一月份营业额为10万元,一季度的营业额共48万元,若平均每月营业额的增长率为x,则根据题意可列方程为( )A、 B、 C、 D、9. 如图,矩形 中, , ,以 为直径的半圆与 相切,连接 . 则阴影部分的面积为( )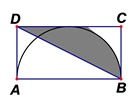 A、 B、 C、 D、10. 如图,在平面直角坐标系 中,矩形 的边 、 分别在x轴和y轴上, , ,点 是 边上一动点,过点D的反比例函数 与边 交于点E.若将 沿 折叠,点B的对应点F恰好落在对角线 上. 则反比例函数的解析式是( )
A、 B、 C、 D、10. 如图,在平面直角坐标系 中,矩形 的边 、 分别在x轴和y轴上, , ,点 是 边上一动点,过点D的反比例函数 与边 交于点E.若将 沿 折叠,点B的对应点F恰好落在对角线 上. 则反比例函数的解析式是( )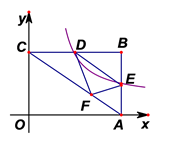 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
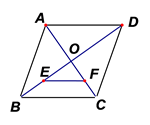
11. 某地白天的温度为 ,夜晚可降到 ,那么该地昼夜的温差为℃.12. 若 ,则 .13. 如图,在菱形 中,对角线 、 交于点O,点E、F分别为 、 中点, , .则 的面积等于 .
 14. 今年五月上旬我市空气质量指数如下表,省外某单位组织了一次退休职工到我市旅游 天,则他们在我市旅游 天时,空气质量都是优良(空气质量指数不大于 表示空气质量优良)的概率是 .
14. 今年五月上旬我市空气质量指数如下表,省外某单位组织了一次退休职工到我市旅游 天,则他们在我市旅游 天时,空气质量都是优良(空气质量指数不大于 表示空气质量优良)的概率是 .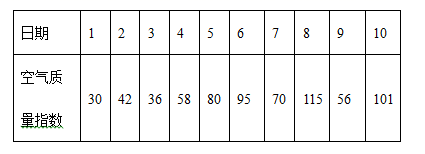 15. 如图,将矩形 沿 折叠,点B落在E点处,连接 .若 ,则 .
15. 如图,将矩形 沿 折叠,点B落在E点处,连接 .若 ,则 .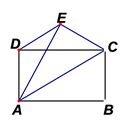 16. 如图,在 中, , ,D是 边上一动点(D不与B、 重合),连接 , 作 ,使 , 交 于点E.当 为等腰三角形时,则 的长为 .
16. 如图,在 中, , ,D是 边上一动点(D不与B、 重合),连接 , 作 ,使 , 交 于点E.当 为等腰三角形时,则 的长为 .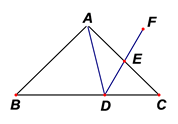
三、解答题
-
17. 计算:18. 关于x、y的方程组 的解为非负数,求m的取值范围.19. 已知 和 是关于x的一元二次方程 的两个不同的实数根.(1)、求k的取值范围;(2)、如果 且k为整数,求k的值.20. 现在,步行运动深受广大健身爱好者的喜爱. 通过“微信运动”可以查询微信好友当天的行走步数.实验中学张老师根据该校 名教师某日“微信运动”中的行走步数,绘制成如下两张统计表(不完整).
步数
频数
频率
a
0.2
19
0.38
b
0.3
4
c
2
0.04
 (1)、写出左表中a、b、c的值,并补全条形统计图;(2)、实验中学所在的某县有 名教师,用张老师调查的样本数据估计该县当天行走步数不少于 步的教师有多少人?(3)、在该校50名教师中,随机选取当天行走步数不少于15000步的2名教师参加“我运动,我健康”的征文活动,求选中的 名教师的行走步数都不小于20000步的概率.21. 如图,在平行四边形 中,点F在 上,连接 ,E为 上一点, .
(1)、写出左表中a、b、c的值,并补全条形统计图;(2)、实验中学所在的某县有 名教师,用张老师调查的样本数据估计该县当天行走步数不少于 步的教师有多少人?(3)、在该校50名教师中,随机选取当天行走步数不少于15000步的2名教师参加“我运动,我健康”的征文活动,求选中的 名教师的行走步数都不小于20000步的概率.21. 如图,在平行四边形 中,点F在 上,连接 ,E为 上一点, .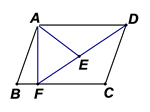 (1)、求证: ∽ ;(2)、若 , , , ,求 的长.22. 如图,我国一艘海监船巡航到海岛A北偏西 方向的P处,发现在海岛A正西方向有一可疑船只B正沿 方向行驶,此时海监船测得,可疑船只B在P处南偏西 方向,距P处 海里,海监船立即从P处沿南偏东 方向驶出.海监船在C处将可疑船只成功拦截.求拦截时可疑船只距海岛A还有多少海里?
(1)、求证: ∽ ;(2)、若 , , , ,求 的长.22. 如图,我国一艘海监船巡航到海岛A北偏西 方向的P处,发现在海岛A正西方向有一可疑船只B正沿 方向行驶,此时海监船测得,可疑船只B在P处南偏西 方向,距P处 海里,海监船立即从P处沿南偏东 方向驶出.海监船在C处将可疑船只成功拦截.求拦截时可疑船只距海岛A还有多少海里?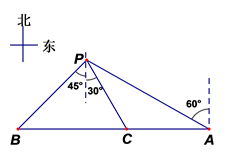 23. 如图,在 中, ,以 为直径作⊙ ,在⊙ 上一点D, .
23. 如图,在 中, ,以 为直径作⊙ ,在⊙ 上一点D, .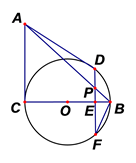 (1)、求证: 是⊙ 的切线;(2)、过D作 分别与 、 和⊙ 交于点P、E、F,若 , .
(1)、求证: 是⊙ 的切线;(2)、过D作 分别与 、 和⊙ 交于点P、E、F,若 , .①求⊙O的半径长;
②直接写出 的长.
24. 如图,在直角坐标系 中,反比例函数 的图象与直线 交于点 , 、 , .连接 、 (1)、求直线 的解析式;(2)、若点C是y轴上的点,当 为等腰三角形时,请直接写出点C的坐标;(3)、求 的面积.25. 如图,在平行四边形 中, , ,P是 上一动点,过P作 的垂线交 于E,将 折叠得到 ,延长 交 于H,连接 .
(1)、求直线 的解析式;(2)、若点C是y轴上的点,当 为等腰三角形时,请直接写出点C的坐标;(3)、求 的面积.25. 如图,在平行四边形 中, , ,P是 上一动点,过P作 的垂线交 于E,将 折叠得到 ,延长 交 于H,连接 . (1)、求证: ;(2)、当 时,证明 是等腰三角形;(3)、若 , ,求 的长.26. 如图,抛物线 与 轴交于点A、B,与y轴交于点 , ,A、B两点间的距离为8,抛物线的对称轴为 .
(1)、求证: ;(2)、当 时,证明 是等腰三角形;(3)、若 , ,求 的长.26. 如图,抛物线 与 轴交于点A、B,与y轴交于点 , ,A、B两点间的距离为8,抛物线的对称轴为 .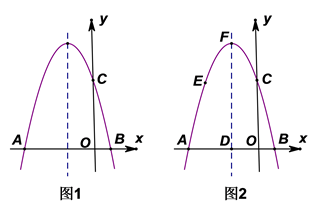 (1)、求抛物线的解析式;(2)、如图1,对称轴上是否存在点P,使 ,若存在,求出点P的坐标;若不存在,请说明理由.(3)、如图2,抛物线的顶点为F,对称轴交x轴于点D,点E为抛物线上一点,点E不与点F重合. 当 时,过点 分别作 轴的垂线和平行线,与 轴交于点Q、与对称轴交于点H,得到矩形 ,求矩形 周长的最大值;
(1)、求抛物线的解析式;(2)、如图1,对称轴上是否存在点P,使 ,若存在,求出点P的坐标;若不存在,请说明理由.(3)、如图2,抛物线的顶点为F,对称轴交x轴于点D,点E为抛物线上一点,点E不与点F重合. 当 时,过点 分别作 轴的垂线和平行线,与 轴交于点Q、与对称轴交于点H,得到矩形 ,求矩形 周长的最大值;