四川省乐山市峨眉山2020年中考数学二模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
1. 比-3大5的数是( )A、 B、 C、 D、2. 某几何体的展开图如图所示,该几何体是( )
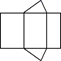 A、三棱柱 B、圆锥 C、四棱柱 D、圆柱3. 下列计算正确的是( )A、 B、 C、 D、4. 将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起,若 ,则 的度数为( )
A、三棱柱 B、圆锥 C、四棱柱 D、圆柱3. 下列计算正确的是( )A、 B、 C、 D、4. 将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起,若 ,则 的度数为( )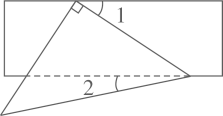 A、 B、 C、 D、5. 为了解学生课外阅读时间情况,随机收集了30名学生一天课外阅读时间,整理如下表:
A、 B、 C、 D、5. 为了解学生课外阅读时间情况,随机收集了30名学生一天课外阅读时间,整理如下表:阅读时间/小时
0.5及以下
0.7
0.9
1.1
1.3
1.5及以上
人数
2
9
6
5
4
4
则本次调查中阅读时间的中位数和众数分别是( )
A、0.7和0.7 B、0.9和0.7 C、1和0.7 D、0.9和1.16. 根据表格对应值:x
1.1
1.2
1.3
1.4
ax2+bx+c
-0.59
0.84
2.29
3.76
判断关于x的方程ax2+bx+c=3的一个解x的范围是( )
A、1.1<x<1.2 B、1.2<x<1.3 C、1.3<x<1.4 D、无法判定7. 如图,已知⊙O是以数轴原点O为圆心,半径为1的圆, ,点P在数轴上运动,若过点P且与 平行的直线与⊙O有公共点,设 ,则x的取值范围是( )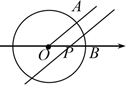 A、 ≤ ≤ B、 ≤ ≤ C、 ≤ ≤ D、 >8. 在平面直角坐标系中,已知 ,设函数 的图像与x轴有M个交点,函数 的图像与x轴有N个交点,则( )A、 或 B、 或 C、 或 D、 或9. 如图,二次函数 的图象过点 ,对称轴为直线 .有以下结论:
A、 ≤ ≤ B、 ≤ ≤ C、 ≤ ≤ D、 >8. 在平面直角坐标系中,已知 ,设函数 的图像与x轴有M个交点,函数 的图像与x轴有N个交点,则( )A、 或 B、 或 C、 或 D、 或9. 如图,二次函数 的图象过点 ,对称轴为直线 .有以下结论:
① ;② ;③若A( ,m), ( ,m)是抛物线上的两点,当 时, ;④点M,N是抛物线与x轴的两个交点,若在x轴下方的抛物线上存在一点P,使得 ⊥ ,则a的取值范围为 ;
⑤若方程 的两根为 , ,且 < ,则﹣2≤ < <4.
其中正确结论的序号是( )
A、①②④ B、①③④ C、①③⑤ D、①②③⑤二、填空题
-
10. 8的立方根是 .11. 若代数式 有意义,则 的取值范围为.12. 已知关于x的一元二次方程mx2+5x+m2﹣2m=0有一个根为0,则m= .13. 如图,扇形 中, , ,C是 的中点, ⊥ 交 于点D,以 为半径的 交 于点E,则图中阴影部分的面积是 .
 14. 已知x,y都是非负数,且满足 ,则 的最大值为 .15. 定义:对于平面直角坐标系 中的线段 和点M,在 中,当 边上的高为2时,称M为 的“等高点”,称此时 为 的“等高距离”.(1)、若点P的坐标为(1,2),点Q的坐标为(4,2),则在点A (1,0), ( ,4),C (0,3)中, 的“等高点”是点;(2)、若 (0,0), =2,当 的“等高点”在y轴正半轴上且“等高距离”最小时,点Q的坐标是 .
14. 已知x,y都是非负数,且满足 ,则 的最大值为 .15. 定义:对于平面直角坐标系 中的线段 和点M,在 中,当 边上的高为2时,称M为 的“等高点”,称此时 为 的“等高距离”.(1)、若点P的坐标为(1,2),点Q的坐标为(4,2),则在点A (1,0), ( ,4),C (0,3)中, 的“等高点”是点;(2)、若 (0,0), =2,当 的“等高点”在y轴正半轴上且“等高距离”最小时,点Q的坐标是 .三、解答题
-
16. 计算: .17. 解方程组18. 如图,在 中, ,D是 的中点,E是 的中点,过点A作 ∥ 交 的延长线于点F,连接 .

求证:
(1)、 ≌ ;(2)、四边形 是菱形.19. 化简 ,并求值,其中x是不等式组 的正整数解.20. 济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.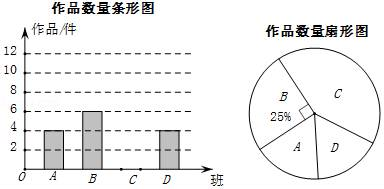
请根据以上信息,回答下列问题:
(1)、杨老师采用的调查方式是(填“普查”或“抽样调查”);(2)、请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .(3)、请估计全校共征集作品的件数.(4)、如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.21. 如图,直线AB:y=kx+b与x轴.y轴分别相交于点A(1,0)和点B(0,2),以线段AB为边在第一象限作正方形ABCD.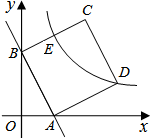 (1)、求直线AB的解析式;(2)、求点D的坐标;(3)、若双曲线 (k>0)与正方形的边CD绐终有一个交点,求k的取值范围.22. 如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.
(1)、求直线AB的解析式;(2)、求点D的坐标;(3)、若双曲线 (k>0)与正方形的边CD绐终有一个交点,求k的取值范围.22. 如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.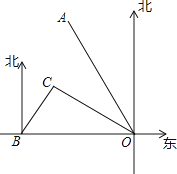 (1)、快艇从港口B到小岛C需要多长时间?(2)、若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.23. 如图,AB是 的直径,D是 的中点, 于E,交CB于点 过点D作BC的平行线DM,连接AC并延长与DM相交于点G.
(1)、快艇从港口B到小岛C需要多长时间?(2)、若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.23. 如图,AB是 的直径,D是 的中点, 于E,交CB于点 过点D作BC的平行线DM,连接AC并延长与DM相交于点G.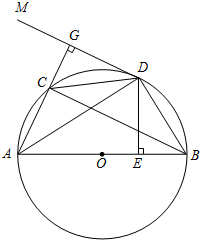 (1)、求证:GD是 的切线;(2)、求证: ;(3)、若 , ,求 的值.24. 已知四边形 中, , ,点E是射线 上一点,F 是射线 上一点,且满足 .(1)、如图,当点 在线段 上时,若 ,在线段 上截取 ,联结 .求证: ;
(1)、求证:GD是 的切线;(2)、求证: ;(3)、若 , ,求 的值.24. 已知四边形 中, , ,点E是射线 上一点,F 是射线 上一点,且满足 .(1)、如图,当点 在线段 上时,若 ,在线段 上截取 ,联结 .求证: ;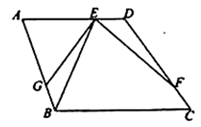 (2)、如图,当点E在线段 的延长线上时,若 , , ,设 , ,求y关于x的函数关系式及其定义域;
(2)、如图,当点E在线段 的延长线上时,若 , , ,设 , ,求y关于x的函数关系式及其定义域; (3)、记 与 交于点 ,在(2)的条件下,若 与 相似,求线段 的长.25. 如图,抛物线 交x轴于A,B两点,交y轴于点C.直线 经过点B,C.
(3)、记 与 交于点 ,在(2)的条件下,若 与 相似,求线段 的长.25. 如图,抛物线 交x轴于A,B两点,交y轴于点C.直线 经过点B,C.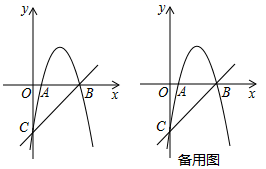 (1)、求抛物线的解析式;(2)、过点A的直线交直线 于点M.
(1)、求抛物线的解析式;(2)、过点A的直线交直线 于点M.①当 时,过抛物线上一动点P(不与点B,C重合),作直线 的平行线交直线 于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接 ,当直线 与直线 的夹角等于 的 倍时,请直接写出点M的坐标.