四川省成都市新都区2020年中考数学三模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
1. 钓鱼岛是中国的固有领土,其渔业资源十分丰富,年捕鱼量达16万吨,数据16万用科学记数法表示为( )A、1.6×104 B、1.6×105 C、16×104 D、16×1052. 如图所示的几何体的左视图为( )
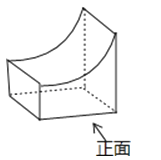 A、
A、 B、
B、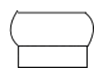 C、
C、 D、
D、 3. 平面直角坐标中,已知点P(a , 3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )A、(﹣a , 3) B、(a , ﹣3) C、(﹣a+2,3) D、(﹣a+4,3)4. 下列计算正确的是( )A、2x2•3x3=6x6 B、x3÷x3=0 C、(2xy)3=6x3y3 D、(x3)m÷x2m=xm5. 如图,已知 , ,下列条件中不能判定 ≌ 的是( )
3. 平面直角坐标中,已知点P(a , 3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )A、(﹣a , 3) B、(a , ﹣3) C、(﹣a+2,3) D、(﹣a+4,3)4. 下列计算正确的是( )A、2x2•3x3=6x6 B、x3÷x3=0 C、(2xy)3=6x3y3 D、(x3)m÷x2m=xm5. 如图,已知 , ,下列条件中不能判定 ≌ 的是( )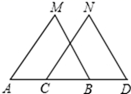 A、 B、 C、 D、6. 如图,是某市一周内最高气温的折线统计图,关于这7天的日气温的说法,错误的是( )
A、 B、 C、 D、6. 如图,是某市一周内最高气温的折线统计图,关于这7天的日气温的说法,错误的是( )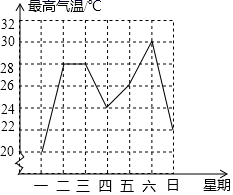 A、最高气温是30℃ B、最低气温是20℃ C、众数是28℃ D、平均数是26℃7. 下列结论正确的是( )A、 是分式方程 B、方程 =1无解 C、方程 的根为x=0 D、解分式方程时,一定会出现增根8. 如图,在平行四边形ABCD中,AB=4,AD=5,∠B=60°,以点B为圆心,BA为半径作圆,交BC边于点E,连接ED,则图中阴影部分的面积为( )
A、最高气温是30℃ B、最低气温是20℃ C、众数是28℃ D、平均数是26℃7. 下列结论正确的是( )A、 是分式方程 B、方程 =1无解 C、方程 的根为x=0 D、解分式方程时,一定会出现增根8. 如图,在平行四边形ABCD中,AB=4,AD=5,∠B=60°,以点B为圆心,BA为半径作圆,交BC边于点E,连接ED,则图中阴影部分的面积为( )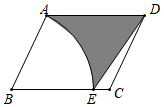 A、9 ﹣ B、9﹣ C、9 D、9﹣9. 关于二次函数 ,以下结论:①抛物线交x轴有两个不同的交点;②不论k取何值,抛物线总是经过一个定点;③设抛物线交x轴于A、B两点,若 ,则 ;④抛物线的顶点在 图象上;⑤抛物线交y轴于C点,若 是等腰三角形,则 ,0,1.其中正确的序号是( )A、①②⑤ B、②③④ C、①④⑤ D、②④10. 如图,在圆内接四边形ABCD中,∠C=110°,则∠BOD的度数为( )
A、9 ﹣ B、9﹣ C、9 D、9﹣9. 关于二次函数 ,以下结论:①抛物线交x轴有两个不同的交点;②不论k取何值,抛物线总是经过一个定点;③设抛物线交x轴于A、B两点,若 ,则 ;④抛物线的顶点在 图象上;⑤抛物线交y轴于C点,若 是等腰三角形,则 ,0,1.其中正确的序号是( )A、①②⑤ B、②③④ C、①④⑤ D、②④10. 如图,在圆内接四边形ABCD中,∠C=110°,则∠BOD的度数为( )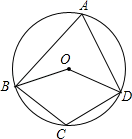 A、140° B、70° C、80° D、60°
A、140° B、70° C、80° D、60°二、填空题
-
11. 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是 .
 12. 一个等腰三角形的两条边分别是6厘米和8厘米,那么它的周长是厘米.13. 把只有颜色不同的2个红球和1个白球装入一个不透明的口袋里搅匀,从中随机地一次摸出2个球,得1个红球1个白球的概率为 .14. 已知线段a、b、c , 如果a:b:c=1:2:3,那么“ ”的值是 .15. 已知关于x、y的方程组 中,x、y满足关系式2x﹣y=5,则代数式a﹣a2的值为 .16. 四个全等的直角三角形按图示方式围成正方行ABCD,过各较长直角边的中点作垂线,围成面积为4的小正方形EFGH,已知AM为Rt△ABM的较长直角边,AM= EF,则正方形ABCD的面积为.
12. 一个等腰三角形的两条边分别是6厘米和8厘米,那么它的周长是厘米.13. 把只有颜色不同的2个红球和1个白球装入一个不透明的口袋里搅匀,从中随机地一次摸出2个球,得1个红球1个白球的概率为 .14. 已知线段a、b、c , 如果a:b:c=1:2:3,那么“ ”的值是 .15. 已知关于x、y的方程组 中,x、y满足关系式2x﹣y=5,则代数式a﹣a2的值为 .16. 四个全等的直角三角形按图示方式围成正方行ABCD,过各较长直角边的中点作垂线,围成面积为4的小正方形EFGH,已知AM为Rt△ABM的较长直角边,AM= EF,则正方形ABCD的面积为.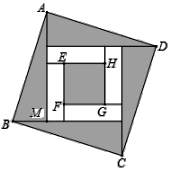 17. 阅读下列材料,然后回答问题:
17. 阅读下列材料,然后回答问题:已知a>0,S1= ,S2=﹣S1﹣1,S3= ,S4=﹣S3﹣1,S5= ,….当n为大于1的奇数时,Sn= ;当n为大于1的偶数时,Sn=﹣Sn﹣1﹣1.直接写出S2020=(用含a的代数式表示);计算:S1+S2+S3+…+S2022= .
18. 如图平面直角坐标系中放置Rt△PEF , ∠E=90°,EP=EF , △PEF绕点P(﹣1,﹣3)转动,PE、PF所在直线分别交y轴,x轴正半轴于点B(0,b),A(a , 0),作矩形AOBC , 双曲线y= (k>0)经过C点,当a , b均为正整数时,k= .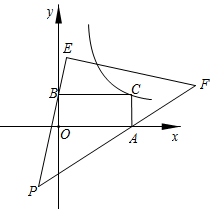
三、解答题
-
19.(1)、计算:﹣22+ ﹣2cos30°+|1﹣ |;(2)、化简:( ﹣1)÷ .20. 已知关于x的一元二次方程kx2﹣4x+2=0有两个不相等的实数根,求k的取值范围.21. 某校随机抽查了部分九年级女生进行1分钟仰卧起坐测试,并将测试的结果绘制成了如图的不完整的统计表和频数分布直方图(注:在频数分布直方图中,每组含左端点,但不含右端点):
仰卧起坐次数的范围(次)
15~20
20~25
25~30
30~35
频数
3
10
12
频率
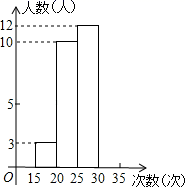 (1)、30~35的频数是、25~30的频率是 . 并把统计图补充完整;(2)、被抽查的所有女同学仰卧起坐次数的中位数是多少?22. 京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D , 先用卷尺量出AB=180m , CD=60m , 再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
(1)、30~35的频数是、25~30的频率是 . 并把统计图补充完整;(2)、被抽查的所有女同学仰卧起坐次数的中位数是多少?22. 京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D , 先用卷尺量出AB=180m , CD=60m , 再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).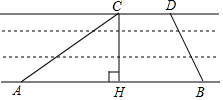 23. 如图,在平面直角坐标系中,一次函数 与反比例函数 的图象相交于 两点,过点 作 轴于点D, , ,B点的坐标为 .
23. 如图,在平面直角坐标系中,一次函数 与反比例函数 的图象相交于 两点,过点 作 轴于点D, , ,B点的坐标为 .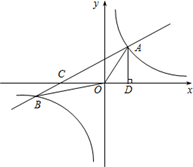 (1)、求一次函数和反比例函数的表达式;(2)、求 的面积;(3)、P是y轴上一点,且 是等腰三角形,请直接写出所有符合条件的P点坐标.24. 如图,AB 是⊙O的直径,∠DAB的角平分线AC交⊙O于点C , 过点C作CD⊥AD于D , AB的延长线与DC的延长线相交于点P , ∠ACB的角平分线CE交AB于点F、交⊙O于E .
(1)、求一次函数和反比例函数的表达式;(2)、求 的面积;(3)、P是y轴上一点,且 是等腰三角形,请直接写出所有符合条件的P点坐标.24. 如图,AB 是⊙O的直径,∠DAB的角平分线AC交⊙O于点C , 过点C作CD⊥AD于D , AB的延长线与DC的延长线相交于点P , ∠ACB的角平分线CE交AB于点F、交⊙O于E .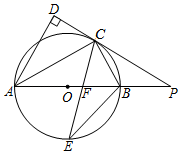 (1)、求证:PC与⊙O相切;(2)、求证:PC=PF;(3)、若AC=8,tan∠ABC= ,求线段BE的长.25. 如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20 ,MD=14 ,求则 NE 的长
(1)、求证:PC与⊙O相切;(2)、求证:PC=PF;(3)、若AC=8,tan∠ABC= ,求线段BE的长.25. 如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20 ,MD=14 ,求则 NE 的长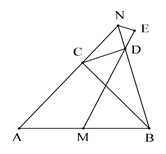 26. 一家蔬菜公司计划到某绿色蔬菜基地收购A,B两种蔬菜共140吨,预计两种蔬菜销售后获利的情况如表所示:
26. 一家蔬菜公司计划到某绿色蔬菜基地收购A,B两种蔬菜共140吨,预计两种蔬菜销售后获利的情况如表所示:销售品种
A种蔬菜
B种蔬菜
每吨获利(元)
1200
1000
其中A种蔬菜的5%、B种蔬菜的3%须运往C市场销售,但C市场的销售总量不超过5.8吨.设销售利润为W元(不计损耗),购进A种蔬菜x吨.
(1)、求W与x之间的函数关系式;(2)、将这140吨蔬菜全部销售完,最多可获得多少利润?27. 如图,菱形ABCD的边长为20cm , ∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q先以2 cm/s的速度沿A→O的路线向点O运动,然后再以2cm/s的速度沿O→D的路线向点D运动,当P、Q到达终点时,整个运动随之结束,设运动时间为t秒.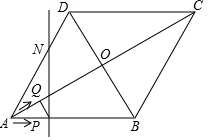 (1)、在点P在AB上运动时,判断PQ与对角线AC的位置关系,并说明理由;(2)、若点Q关于菱形ABCD的对角线交点O的对称点为M , 过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N .
(1)、在点P在AB上运动时,判断PQ与对角线AC的位置关系,并说明理由;(2)、若点Q关于菱形ABCD的对角线交点O的对称点为M , 过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N .①直接写出当△PQM是直角三角形时t的取值范围;
②是否存在这样的t , 使△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
28. 已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.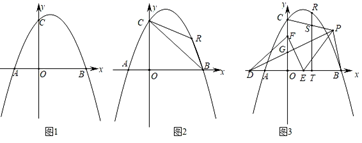 (1)、如图1,求抛物线的解析式;(2)、如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;(3)、在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS= ,求点R的坐标.
(1)、如图1,求抛物线的解析式;(2)、如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;(3)、在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS= ,求点R的坐标.