四川省成都市青白江区2020年中考数学三模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
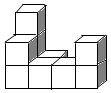
1. 如图是由相同小正方体组成的立体图形,其俯视图为( )
 A、
A、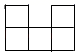 B、
B、 C、
C、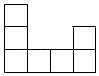 D、
D、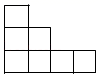 2. 花粉的质量很小,一粒某种花粉的质量约为0.000103毫克,那么0.000103可用科学记数法表示为( )A、 B、 C、 D、3. 下面四个图形中,∠1=∠2一定成立的是( )A、
2. 花粉的质量很小,一粒某种花粉的质量约为0.000103毫克,那么0.000103可用科学记数法表示为( )A、 B、 C、 D、3. 下面四个图形中,∠1=∠2一定成立的是( )A、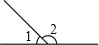 B、
B、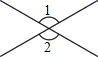 C、
C、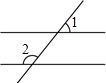 D、
D、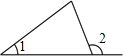 4. 若点P(m﹣1,5)与点Q (3,2﹣n)关于y轴对称,则m+n的值是( )A、﹣5 B、1 C、5 D、115. 如图是某市一周以来新冠肺炎疑似病例数的统计图,则这七天疑似病例数的中位数和众数分别是( )
4. 若点P(m﹣1,5)与点Q (3,2﹣n)关于y轴对称,则m+n的值是( )A、﹣5 B、1 C、5 D、115. 如图是某市一周以来新冠肺炎疑似病例数的统计图,则这七天疑似病例数的中位数和众数分别是( )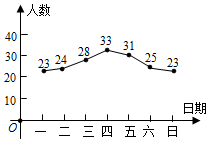 A、中位数是25,众数是23 B、中位数是33,众数是23 C、中位数是25,众数是33 D、中位数是33,众数是336. 下列计算正确的是( )A、a3+a3=a6 B、a3•a2=a6 C、a3÷a=a2 D、(﹣a3)2=﹣a67. 解分式方程 ,可知方程( )A、解为 B、解为 C、解为 D、无解8. 若一个正六边形的半径为2,则它的边心距等于( )A、2 B、1 C、 D、29. 已知二次函数 的图象如图所示,给出以下结论:① ;②b2-4ac<0;③ ;④ c<0.其中所有正确结论的序号是( )
A、中位数是25,众数是23 B、中位数是33,众数是23 C、中位数是25,众数是33 D、中位数是33,众数是336. 下列计算正确的是( )A、a3+a3=a6 B、a3•a2=a6 C、a3÷a=a2 D、(﹣a3)2=﹣a67. 解分式方程 ,可知方程( )A、解为 B、解为 C、解为 D、无解8. 若一个正六边形的半径为2,则它的边心距等于( )A、2 B、1 C、 D、29. 已知二次函数 的图象如图所示,给出以下结论:① ;②b2-4ac<0;③ ;④ c<0.其中所有正确结论的序号是( )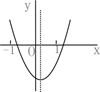 A、③④ B、②③ C、①④ D、①②
A、③④ B、②③ C、①④ D、①②二、填空题
-
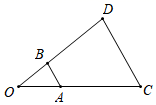
10. 因式分解:m2n﹣9n= .11. 如图,以点O为位似中心,将 放大后得到 , ,则 .
 12. 一次函数y=(3﹣k)x+1的图象与x轴的交点在正半轴上,则k的取值范围 .13. 如图,在△ABC中,按以下步骤作图:①分别以点B和点C为圆心,大于 BC的长为半径作弧,两弧相交于点M和N;②作直线MN , 分别交边AB , BC于点D和E , 连接CD . 若∠BCA=90°,AB=8,则CD的长为 .
12. 一次函数y=(3﹣k)x+1的图象与x轴的交点在正半轴上,则k的取值范围 .13. 如图,在△ABC中,按以下步骤作图:①分别以点B和点C为圆心,大于 BC的长为半径作弧,两弧相交于点M和N;②作直线MN , 分别交边AB , BC于点D和E , 连接CD . 若∠BCA=90°,AB=8,则CD的长为 .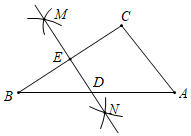 14. 若关于x、y的二元一次方程组 的解是二元一次方程的 的解,则k的值为.15. 比较大小: (填“>”,“<”,或“=”).16. 如图,已知⊙O的两条直径AB、EF互相垂直,AC=BD , 和 所对的圆心角都为120°,且 = .现随机地向该图形内掷一枚小针,记针尖落在 和 所围封闭区域内的概率为P1 , 针尖落在⊙O内的概率为P2 , 则 = .
14. 若关于x、y的二元一次方程组 的解是二元一次方程的 的解,则k的值为.15. 比较大小: (填“>”,“<”,或“=”).16. 如图,已知⊙O的两条直径AB、EF互相垂直,AC=BD , 和 所对的圆心角都为120°,且 = .现随机地向该图形内掷一枚小针,记针尖落在 和 所围封闭区域内的概率为P1 , 针尖落在⊙O内的概率为P2 , 则 = .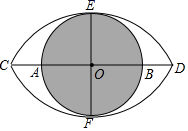 17. 如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE= ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.
17. 如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE= ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为.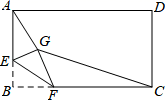 18. 如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ;….按此规律继续旋转,直至得到点P2020为止,则AP2020= .
18. 如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ;….按此规律继续旋转,直至得到点P2020为止,则AP2020= .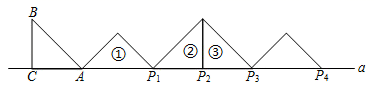
三、解答题
-
19.(1)、计算: ﹣( )﹣1+| ﹣2|﹣2cos45°;(2)、解不等式组: .20. 化简,求值: ÷(1﹣ ),其中x=3.21. 某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A篮球;B乒乓球;C羽毛球;D足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
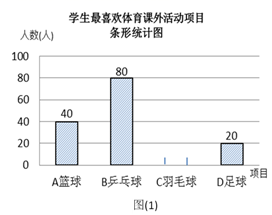
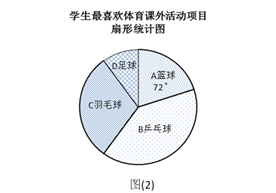 (1)、这次被调查的学生共有人;(2)、请你将条形统计图(1)补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)22. 如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的长度是12.5米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角∠CAQ为45°,坡角∠BAQ为37°,求二楼的层高BC(精确到0.1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 )
(1)、这次被调查的学生共有人;(2)、请你将条形统计图(1)补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)22. 如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的长度是12.5米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角∠CAQ为45°,坡角∠BAQ为37°,求二楼的层高BC(精确到0.1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 )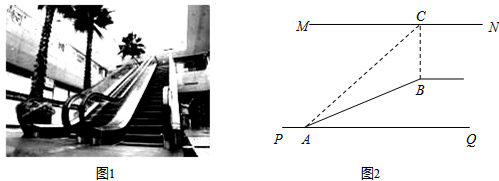 23. 如图,一次函数y=kx+1与反比例函数y= 的图象相交于A(2,3),B两点.
23. 如图,一次函数y=kx+1与反比例函数y= 的图象相交于A(2,3),B两点.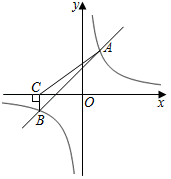 (1)、求k、m的值和B点坐标;(2)、过点B作BC⊥x轴于C , 连接AC , 将△ABC沿x轴向右平移,对应得到△A'B'C',当反比例函数图象经过A'C'的中点M时,求△MAC的面积.24. 如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧 的中点,连结AD并延长,与过C点的直线交于P , OD与BC相交于点E .
(1)、求k、m的值和B点坐标;(2)、过点B作BC⊥x轴于C , 连接AC , 将△ABC沿x轴向右平移,对应得到△A'B'C',当反比例函数图象经过A'C'的中点M时,求△MAC的面积.24. 如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧 的中点,连结AD并延长,与过C点的直线交于P , OD与BC相交于点E .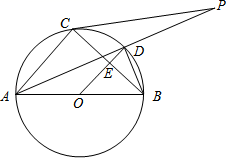 (1)、求证:OE= AC;(2)、连接CD , 若∠PCD=∠PAC , 试判断直线PC与⊙O的位置关系,并说明理由.(3)、在(2)的条件下,当AC=6,AB=10时,求切线PC的长.25. 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)、求证:OE= AC;(2)、连接CD , 若∠PCD=∠PAC , 试判断直线PC与⊙O的位置关系,并说明理由.(3)、在(2)的条件下,当AC=6,AB=10时,求切线PC的长.25. 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.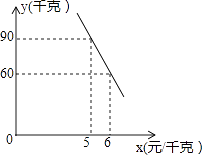 (1)、根据题意,填写如表:(2)、经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;(3)、若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?26. 如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)、根据题意,填写如表:(2)、经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;(3)、若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?26. 如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.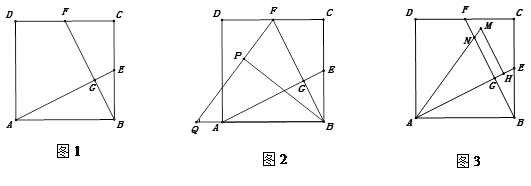 (1)、求证:AE⊥BF;(2)、将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;(3)、将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的边长为4时,直接写出四边形GHMN的面积.27. 如图,抛物线y=ax2+bx+3(a≠0)与x轴,y轴分别交于点A(﹣1,0),B(3,0),点C三点.
(1)、求证:AE⊥BF;(2)、将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;(3)、将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的边长为4时,直接写出四边形GHMN的面积.27. 如图,抛物线y=ax2+bx+3(a≠0)与x轴,y轴分别交于点A(﹣1,0),B(3,0),点C三点.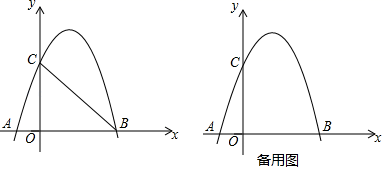 (1)、求抛物线的解析式;(2)、x轴上是否存在点P,使PC+ PB最小?若存在,请求出点P的坐标及PC+ PB的最小值;若不存在,请说明理由;(3)、连接BC,设E为线段BC中点.若M是抛物线上一动点,将点M绕点E旋转180°得到点N,当以B、C、M、N为顶点的四边形是矩形时,直接写出点N的坐标.
(1)、求抛物线的解析式;(2)、x轴上是否存在点P,使PC+ PB最小?若存在,请求出点P的坐标及PC+ PB的最小值;若不存在,请说明理由;(3)、连接BC,设E为线段BC中点.若M是抛物线上一动点,将点M绕点E旋转180°得到点N,当以B、C、M、N为顶点的四边形是矩形时,直接写出点N的坐标.