湖南省永州市2020年中考数学4月模拟试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
1. 下列实数2,π, ,0中,最小的数是( )A、2 B、 C、﹣π D、02. 下列计算中正确的是( )A、a2+b3=2a5 B、a4÷a=a4 C、a2•a4=a8 D、(﹣a2)3=﹣a63. 如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )
 A、
A、 B、
B、 C、
C、 D、
D、 4.
4.如图,直线AB与CD相交于点O,过点O作OE⊥AB,若∠1=35°,则∠2的度数是( )
 A、45° B、55° C、65° D、75°5. 现有一数据:3,4,5,5,6,6,6,7,则下列说法正确的是( ).A、众数是5和6 B、众数是5.5 C、中位数是5.5 D、中位数是66. 不等式组 的解集在数轴上表示正确的是( )A、
A、45° B、55° C、65° D、75°5. 现有一数据:3,4,5,5,6,6,6,7,则下列说法正确的是( ).A、众数是5和6 B、众数是5.5 C、中位数是5.5 D、中位数是66. 不等式组 的解集在数轴上表示正确的是( )A、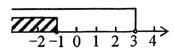 B、
B、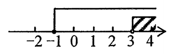 C、
C、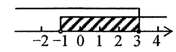 D、
D、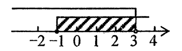 7. 半径为10的 中,弦 ,则点O到弦AB的距离为A、10 B、8 C、6 D、58. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②2a+b=0;③3a+c>0;④4a﹣2b+c<0:⑤9a+3b+c<0.其中结论正确的个数有( )
7. 半径为10的 中,弦 ,则点O到弦AB的距离为A、10 B、8 C、6 D、58. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②2a+b=0;③3a+c>0;④4a﹣2b+c<0:⑤9a+3b+c<0.其中结论正确的个数有( ) A、1个 B、2个 C、3个 D、4个9. 如图,点A在反比例函数y= (x>0)的图象上,点B在反比例函数y= (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C , 连接AC , 若△ABC的面积是6,则k的值为( )
A、1个 B、2个 C、3个 D、4个9. 如图,点A在反比例函数y= (x>0)的图象上,点B在反比例函数y= (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C , 连接AC , 若△ABC的面积是6,则k的值为( ) A、10 B、12 C、14 D、1610. 如图,边长为4和10的两个正方形ABCD与CEFG并排在一起,连接BD并延长交EF于H,交EG于I,则GI的长为( )
A、10 B、12 C、14 D、1610. 如图,边长为4和10的两个正方形ABCD与CEFG并排在一起,连接BD并延长交EF于H,交EG于I,则GI的长为( ) A、3 B、7 C、3 D、7
A、3 B、7 C、3 D、7二、解答题
-
11. 2019年华为发布 “鲲鹏920”计算芯片:64核心业内性能最强! 也就是0.000000007 ,数据0.000000007 可以用科学记数法表示为m.12. 计算:|1﹣2cos30°|+ ﹣(﹣ )﹣1﹣(5﹣π)013. 先化简,再求值: ,其中 .14. 游泳是一项深受青少年喜爱的体育运动,某中学为了加强学生的游泳安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的 名学生中作了抽样调查.制作了下面两个不完整的统计图.请根据这两个统计图回答以下问题:
 (1)、这次抽样调查中,共调查了名学生;(2)、补全两个统计图;(3)、根据抽样调查的结果,估算该校 名学生中大约有多少人“结伴时会下河学游泳”?15. 为了维护国家主权和海洋权利,我国海监部门对中国海域实现常态化管理.某日,我国海监船在某海岛附近的海域执行巡逻任务.如图,此时海监船位于海岛P的北偏东30°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的南偏东45°方向的B处,求海监船航行了多少海里(结果保留根号)?
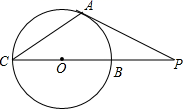
(1)、这次抽样调查中,共调查了名学生;(2)、补全两个统计图;(3)、根据抽样调查的结果,估算该校 名学生中大约有多少人“结伴时会下河学游泳”?15. 为了维护国家主权和海洋权利,我国海监部门对中国海域实现常态化管理.某日,我国海监船在某海岛附近的海域执行巡逻任务.如图,此时海监船位于海岛P的北偏东30°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的南偏东45°方向的B处,求海监船航行了多少海里(结果保留根号)?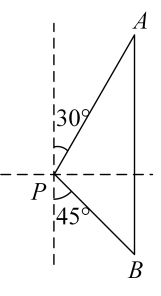 16. 某服装店用4000元购进一批某品牌的文化衫若干件,很快售完,该店又用6300元钱购进第二批这种文化衫,所进的件数比第一批多40%,每件文化衫的进价比第一批每件文化衫的进价多10元,请解答下列问题:(1)、求购进的第一批文化衫的件数;(2)、为了取信于顾客,在这两批文化衫的销售中,售价保持了一致.若售完这两批文化衫服装店的总利润不少于4100元钱,那么服装店销售该品牌文化衫每件的最低售价是多少元?17. 如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.
16. 某服装店用4000元购进一批某品牌的文化衫若干件,很快售完,该店又用6300元钱购进第二批这种文化衫,所进的件数比第一批多40%,每件文化衫的进价比第一批每件文化衫的进价多10元,请解答下列问题:(1)、求购进的第一批文化衫的件数;(2)、为了取信于顾客,在这两批文化衫的销售中,售价保持了一致.若售完这两批文化衫服装店的总利润不少于4100元钱,那么服装店销售该品牌文化衫每件的最低售价是多少元?17. 如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.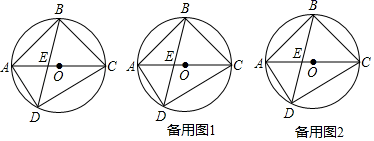 (1)、求∠ADB的度数;(2)、过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;(3)、在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.18.(1)、(学习心得)
(1)、求∠ADB的度数;(2)、过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;(3)、在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.18.(1)、(学习心得)于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.

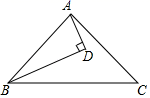
例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数.若以点A为圆心,AB为半径作辅助⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC=°.
(2)、(问题解决)如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=25°,求∠BAC的度数.
(3)、(问题拓展)如图3,如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
19. 如图,在平面直角坐标系内,抛物线 与x轴交于点A,C(点A在点C的左侧),与y轴交于点B,顶点为D.点Q为线段BC的三等分点(靠近点C). (1)、点M为抛物线对称轴上一点,点E为对称轴右侧抛物线上的点且位于第一象限,当 的周长最小时,求 面积的最大值;(2)、在(1)的条件下,当 的面积最大时,过点E作 轴,垂足为N,将线段CN绕点C顺时针旋转90°得到点N,再将点N向上平移 个单位长度.得到点P,点G在抛物线的对称轴上,请问在平面直角坐标系内是否存在一点H,使点D,P,G,H构成菱形.若存在,请直接写出点H的坐标,若不存在,请说明理由.
(1)、点M为抛物线对称轴上一点,点E为对称轴右侧抛物线上的点且位于第一象限,当 的周长最小时,求 面积的最大值;(2)、在(1)的条件下,当 的面积最大时,过点E作 轴,垂足为N,将线段CN绕点C顺时针旋转90°得到点N,再将点N向上平移 个单位长度.得到点P,点G在抛物线的对称轴上,请问在平面直角坐标系内是否存在一点H,使点D,P,G,H构成菱形.若存在,请直接写出点H的坐标,若不存在,请说明理由.三、填空题
-
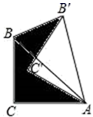
20. 如图,将含有45°角的直角三角板ABC(∠C=90°)绕点A顺时针旋转30°得到△AB′C′,连接BB′,已知AC=2,则阴影部分面积为 .
 21. 如果点A(﹣3,y1)和点B(﹣2,y2)是抛物线y=x2+a上的两点,那么y1y2 . (填“>”、“=”、“<”).22. 在一个不透明的袋中装有黑色和红色两种颜色的球共 个,每个球触颜色外都相同,每次摇匀后随即摸出一个球,记下颜色后再放回袋中,通过大量重复摸球实验后,发现摸到黑球的频率稳定于 ,则可估计这个袋中红球的个数约为.23. 方程x2=2020x的解是 .
21. 如果点A(﹣3,y1)和点B(﹣2,y2)是抛物线y=x2+a上的两点,那么y1y2 . (填“>”、“=”、“<”).22. 在一个不透明的袋中装有黑色和红色两种颜色的球共 个,每个球触颜色外都相同,每次摇匀后随即摸出一个球,记下颜色后再放回袋中,通过大量重复摸球实验后,发现摸到黑球的频率稳定于 ,则可估计这个袋中红球的个数约为.23. 方程x2=2020x的解是 .