湖南省娄底市2020年中考数学5有模拟试卷

试卷更新日期：2020-07-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 2020的倒数是（）

A、-2020 B、2020 C、 $\frac{1}{2020}$ D、 $- \frac{1}{2020}$

查看试题解析
2. 下列运算正确的是（）

A、（ab）²＝a²b² B、a²+a²＝a⁴ C、（a²）³＝a⁵ D、a²•a³＝a⁶

查看试题解析
3. 下列结论中，矩形具有而菱形不一定具有的性质是（）

A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直

查看试题解析
4. 某校5名同学在“国学经典颂读”比赛中，成绩（单位：分）分别是86，95，97，90，88，这组数据的中位数是（）

A、97 B、90 C、95 D、88

查看试题解析
5. 中国华为麒麟985处理器是采用7纳米制程工艺的手机芯片，在指甲盖大小的尺寸上塞进了120亿个晶体管，是世界上最先进的具有人工智能的手机处理器，将120亿个用科学记数法表示为（）

A、 $1.2 \times 10^{9}$ 个 B、 $12 \times 10^{9}$ 个 C、 $1.2 \times 10^{10}$ 个 D、 $1.2 \times 10^{11}$ 个

查看试题解析
6. 下列命题是真命题的是（）

A、两直线平行，同位角相等 B、相似三角形的面积比等于相似比 C、菱形的对角线相等 D、相等的两个角是对顶角

查看试题解析
7. 下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB＝5，BC＝13，CA＝12，则阴影部分(即四边形AEOF)的面积是（）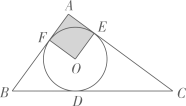

A、4 B、6.25 C、7.5 D、9

查看试题解析
9. 函数y＝ $\frac{1}{x + 1}$ 的大致图象是（）

A、 B、 C、 D、

查看试题解析
10. 如图，直线y=kx+b交坐标轴于A（﹣2，0），B（0，3）两点，则不等式kx+b＞0的解集是（）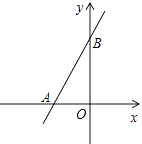

A、x＞3 B、﹣2＜x＜3 C、x＜﹣2 D、x＞﹣2

查看试题解析
11. 已知二次函数y＝ax²+bx+c的图象如图所示，下列结论：①ac＜0，②b﹣2a＜0，③b²﹣4ac＜0，④a﹣b+c＜0，正确的是（）

A、①② B、①④ C、②③ D、②④

查看试题解析
12. 在平面直角坐标系中，一个智能机器人接到的指令是：从原点O出发，按“向上→向右→向下→向右”的方向依次不断移动，每次移动1个单位长度，其移动路程如图所示，第一次移动到点A₁ ，第二次移动到点A₂ ，第n次移动到点A_n ，则点A₂₀₂₀的坐标是（）

A、(1010，0) B、(1010，1) C、(1009，0) D、(1009，1)

查看试题解析

二、填空题

13. 函数y＝ $\frac{4}{x + 1}$ 的自变量x的取值范围是．

查看试题解析
14. 从﹣3,﹣1，π，0，3这五个数中随机抽取一个数，恰好是负数的概率是.

查看试题解析
15. 如图，直线a，b被直线c，d所截．若 $a ∥ b$ ， $∠ 1 = 130^{°}$ ， $∠ 2 = 30^{°}$ ，则 $∠ 3$ 的度数为度．

查看试题解析
16. 如图，AB是⊙O的直径，C、D是⊙O上的两点，∠AOC＝120°，则∠CDB＝°．

查看试题解析
17. 设x₁ ， x₂是一元二次方程x²﹣x﹣1＝0的两根，则x₁+x₂+x₁x₂＝．

查看试题解析
18. 阅读材料：设 $\vec{a}$ ＝（x₁ ， y₁）， $\vec{b}$ ＝（x₂ ， y₂），如果 $\vec{a}$ ∥ $\vec{b}$ ，则x₁•y₂＝x₂•y₁ ，根据该材料填空，已知 $\vec{a}$ ＝（4，3）， $\vec{b}$ ＝（8，m），且 $\vec{a}$ ∥ $\vec{b}$ ，则m＝.

查看试题解析

三、解答题

19. 计算：（π﹣2020）⁰+4sin60°﹣ $\sqrt{12}$ +|﹣3|．

查看试题解析
20. 先化简，再求值： $(\frac{2 x - 3}{x - 2} - 1) \div \frac{x^{2} - 2 x + 1}{x - 2}$ ，然后从0，1，2三个数中选择一个恰当的数代入求值．

查看试题解析
21. 某校为了庆祝建国七十周年，决定举办一台文艺晚会，为了了解学生最喜爱的节目形式，随机抽取了部分学生进行调查，规定每人从“歌曲”，“舞蹈”，“小品”，“相声”和“其它”五个选项中选择一个，并将调查结果绘制成如下两幅不完整的统计图表，请根据图中信息，解答下列题：

最喜爱的节目

人数

歌曲

15

舞蹈

a

小品

12

相声

10

其它

b

(1)、在此次调查中，该校一共调查了名学生；

(2)、a＝；b＝；

(3)、在扇形计图中，计算“歌曲”所在扇形的圆心角的度数；

(4)、若该校共有1200名学生，请你估计最喜爱“相声”的学生的人数．

查看试题解析
22. 如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角为45°，沿斜坡走3 $\sqrt{5}$ 米到达斜坡上点D，在此处测得树顶端点B的仰角为30°，且斜坡AF的坡比为1：2．求大树BC的高度约为多少米？（ $\sqrt{3}$ ≈1.732，结果精确到0.1）

查看试题解析
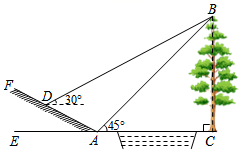23. 为进一步提升学生体质健康水平，我市某校计划用400元购买10个体育用品，备选体育用品及单价如表：

备用体育用品

足球

篮球

排球

单价（元）

50

40

25

(1)、若400元全部用来购买足球和排球共10个，则足球和排球各买多少个；

(2)、若学校先用一部分资金购买了a个排球，再用剩下的资金购买了相同数量的足球和篮球，此时正好剩余30元，求a的值．

查看试题解析
24. 如图，△ABC内接于⊙O，AC＝BC，CD是⊙O的直径，与AB相交于点G，过点D作EF∥AB，分别交CA、CB的延长线于点E、F，连接BD.

(1)、求证：EF是⊙O的切线；

(2)、求证：BD²＝AC•BF.

查看试题解析
25. 如图，过线段AB的端点B作射线BG⊥AB，P为射线BG上一点，以AP为边作正方形APCD，且点C、D与点B在AP两侧，在线段DP上取一点E，使∠EAP＝∠BAP，直线CE与线段AB相交于点F（点F与点A、B不重合）．

(1)、求证： $△ A E P$ ≌ $△ C E P$ ；

(2)、判断CF与AB的位置关系，并说明理由；

(3)、试探究AE+EF+AF与2AB是否相等，并说明理由．

查看试题解析
26. 如图，二次函数y＝ax²+bx+2的图象与x轴相交于点A（﹣1，0）、B（4，0），与y轴相交于点C ．

(1)、求该函数的表达式；

(2)、点P为该函数在第一象限内的图象上一点，过点P作PQ⊥BC ，垂足为点Q ，连接PC ．
①求线段PQ的最大值；

②若以点P、C、Q为顶点的三角形与△ABC相似，求点P的坐标．

查看试题解析

最喜爱的节目	人数
歌曲	15
舞蹈	a
小品	12
相声	10
其它	b

备用体育用品	足球	篮球	排球
单价（元）	50	40	25