湖南省怀化市2020年中考数学6月模拟试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
1. -2的倒数是( )A、-2 B、 C、 D、22. 下列计算正确的是( )A、(a3)3=a6 B、a6÷a3=a2 C、2a+3b=5ab D、a2•a3=a53. 如图所示的几何体的俯视图是( )
 A、
A、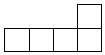 B、
B、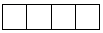 C、
C、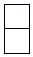 D、
D、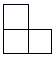 4. 若单项式2x2ya+b与- xa-by4是同类项,则a,b的值分别为( )A、a=3,b=1 B、a=-3,b=1 C、a=3,b=-1 D、a=-3,b=-15. 函数 中,自变量x的取值范围是( )A、 B、 C、 D、6. 某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
4. 若单项式2x2ya+b与- xa-by4是同类项,则a,b的值分别为( )A、a=3,b=1 B、a=-3,b=1 C、a=3,b=-1 D、a=-3,b=-15. 函数 中,自变量x的取值范围是( )A、 B、 C、 D、6. 某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A、560(1+x)2=315 B、560(1-x)2=315 C、560(1-2x)2=315 D、560(1-x2)=3157. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是( )A、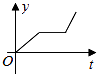 B、
B、 C、
C、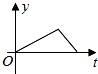 D、
D、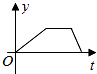 8. 下列说法中正确的是( )A、“打开电视,正在播放新闻节目”是必然事件 B、“抛一枚硬币,正面进上的概率为 ”表示每抛两次就有一次正面朝上 C、“抛一枚均匀的正方体骰子,朝上的点数是6的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在 附近 D、为了解某种节能灯的使用寿命,选择全面调查9. 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
8. 下列说法中正确的是( )A、“打开电视,正在播放新闻节目”是必然事件 B、“抛一枚硬币,正面进上的概率为 ”表示每抛两次就有一次正面朝上 C、“抛一枚均匀的正方体骰子,朝上的点数是6的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在 附近 D、为了解某种节能灯的使用寿命,选择全面调查9. 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )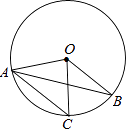 A、25° B、50° C、60° D、30°10. 已知二次函数 ( )的图象如图所示,对称轴是直线 ,下列结论:①abc<0;②2a+b=0;③a﹣b+c>0;④4a﹣2b+c<0
A、25° B、50° C、60° D、30°10. 已知二次函数 ( )的图象如图所示,对称轴是直线 ,下列结论:①abc<0;②2a+b=0;③a﹣b+c>0;④4a﹣2b+c<0其中正确的是( )
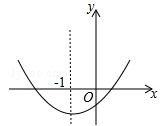 A、①② B、只有① C、③④ D、①④
A、①② B、只有① C、③④ D、①④二、填空题
-
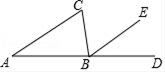
11. 如图,在△ABC中,∠ABC=80°,∠C=70°,且BE∥AC,则∠EBD= .
 12. 如图,菱形的周长是 , ,则 .
12. 如图,菱形的周长是 , ,则 .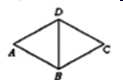 13. 从巴中市交通局获悉,我市2015年前4月在巴陕高速公路完成投资8400万元,请你将8400万元用科学记数记表示为 元.14. 分解因式: .15. 若a、b、c为三角形的三边,且a、b满足 ,则第三边c的取值范围是 .16. 分式方程=的解为x= .
13. 从巴中市交通局获悉,我市2015年前4月在巴陕高速公路完成投资8400万元,请你将8400万元用科学记数记表示为 元.14. 分解因式: .15. 若a、b、c为三角形的三边,且a、b满足 ,则第三边c的取值范围是 .16. 分式方程=的解为x= .
三、解答题
-
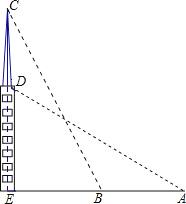
17. 解二元一次方程组: .18. 如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,≈1.7,≈1.4 ).
 19. 中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
19. 中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题: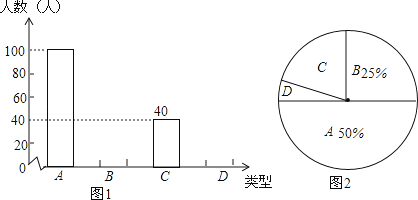 (1)、此次抽样调查中,共调查了 名学生.
(1)、此次抽样调查中,共调查了 名学生.
(2)、将图1、图2补充完整;
(3)、现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).20. 如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.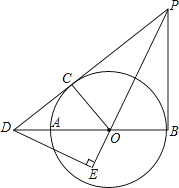 (1)、求证:PB是的切线;
(1)、求证:PB是的切线;
(2)、若PB=6,DB=8,求⊙O的半径21. 如图,直线y=-2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.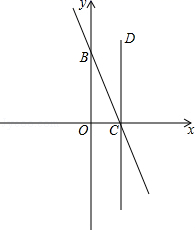 22. 李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
22. 李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)、求李老师步行的平均速度;
(2)、请你判断李老师能否按时上班,并说明理由.
23. 如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.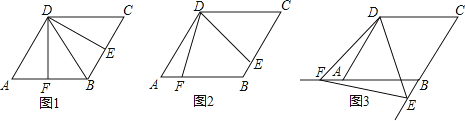 (1)、继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由(2)、再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(1)、继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由(2)、再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)、连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?24. 已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.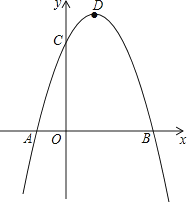 (1)、求此二次函数解析式;(2)、连接DC、BC、DB,求证:△BCD是直角三角形;(3)、在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
(1)、求此二次函数解析式;(2)、连接DC、BC、DB,求证:△BCD是直角三角形;(3)、在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.