湖南省郴州市桂阳县2020年中考数学5月模拟试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 函数y= 中,自变量x的取值范围是( )A、x≥﹣1 B、x>﹣1 C、x≠﹣1 D、x>13. 据相关报道,开展精准扶贫工作五年以来,我国约有55000000人摆脱贫困,将55000000用科学记数法表示是( )A、55×106 B、0.55×108 C、5.5×106 D、5.5×1074. 在下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列各式中,计算正确的是( )A、6a﹣2b=4ab B、(a2)3=a5 C、a8÷a4=a2 D、a2•a=a36.
5. 下列各式中,计算正确的是( )A、6a﹣2b=4ab B、(a2)3=a5 C、a8÷a4=a2 D、a2•a=a36.如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
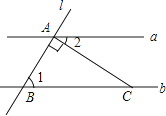 A、58° B、42° C、32° D、28°7. 某校5名同学在“国学经典颂读”比赛中,成绩(单位:分)分别是86,95,97,90,88,这组数据的中位数是( )A、97 B、90 C、95 D、888. 正方形ABCD的边长AB=2,E为AB的中点,F为BC的中点,AF分别与DE、BD相交于点M , N , 则MN的长为( )
A、58° B、42° C、32° D、28°7. 某校5名同学在“国学经典颂读”比赛中,成绩(单位:分)分别是86,95,97,90,88,这组数据的中位数是( )A、97 B、90 C、95 D、888. 正方形ABCD的边长AB=2,E为AB的中点,F为BC的中点,AF分别与DE、BD相交于点M , N , 则MN的长为( )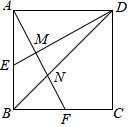 A、 B、 ﹣1 C、 D、
A、 B、 ﹣1 C、 D、二、填空题
-
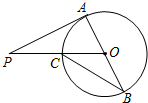
9. 分解因式:4x3﹣16x=.10. 在一个不透明的袋子里装有3个白色乒乓球和若干个黄色乒乓球,若从这个袋子里随机摸岀一个乒乓球,恰好是黄球的概率为 ,则袋子内共有乒乓球的个数为 .11. 计算: + = .12. AB是⊙O的直径,PA切⊙O于点A , PO交⊙O于点C;连接BC , 若∠P=40°,则∠B等于 .
 13. 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为 .
13. 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为 .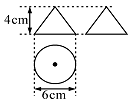 14. 一个三角形的两边长分别为3和6,第三边长是方程x2-10x+21=0的根,则三角形的周长为.15. 从甲、乙、丙、丁四人中选一人参加诗词大会比赛,经过三轮初赛,他们的平均成绩都是86.5分,方差分别是S甲2=1.5,S乙2=2.6,S丙2=3.5,S丁2=3.68,你认为派去参赛更合适.16. 如图,在平面直角坐标系中,点A1 , A2 , A3…和B1 , B2 , B3 , …分别在直线y= x+b和x轴上.△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是 .
14. 一个三角形的两边长分别为3和6,第三边长是方程x2-10x+21=0的根,则三角形的周长为.15. 从甲、乙、丙、丁四人中选一人参加诗词大会比赛,经过三轮初赛,他们的平均成绩都是86.5分,方差分别是S甲2=1.5,S乙2=2.6,S丙2=3.5,S丁2=3.68,你认为派去参赛更合适.16. 如图,在平面直角坐标系中,点A1 , A2 , A3…和B1 , B2 , B3 , …分别在直线y= x+b和x轴上.△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是 .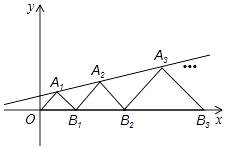 17. 观察下列等式:
17. 观察下列等式:第一个等式: ;
第二个等式: ;
第三个等式: ;
第四个等式: ;
按上述规律,回答下列问题:
(1)、请写出第六个等式:a6==;(2)、用含n的代数式表示第n个等式:an==;(3)、a1+a2+a3+a4+a5+a6=(得出最简结果);(4)、计算:a1+a2+…+an .三、解答题
-
18. 计算: .19. 解不等式组 ,并把解集在数轴上表示出来.20. 如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.
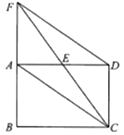 (1)、求证:四边形ACDF是平行四边形;(2)、当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.21. 某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
(1)、求证:四边形ACDF是平行四边形;(2)、当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.21. 某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
请根据以上信息,解答下列问题:
(1)、这次被调查的学生共有多少人?
(2)、请将条形统计图补充完整;(3)、若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?(4)、该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)22. 科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60方向行驶8千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C , 小明发现古镇C恰好在A地的正北方向,求B , C两地的距离.(结果保留根号)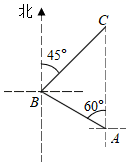 23. 某商店购进A、B两种商品,购买1个A商品比购买1个B商品多花10元,并且花费300元购买A商品和花费100元购买B商品的数量相等.(1)、求购买一个A商品和一个B商品各需要多少元;(2)、商店准备购买A、B两种商品共80个,若A 商品的数量不少于B商品数量的4倍,并且购买A、B商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?24. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D , 点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D , 分别交AC , AB于点E , F .
23. 某商店购进A、B两种商品,购买1个A商品比购买1个B商品多花10元,并且花费300元购买A商品和花费100元购买B商品的数量相等.(1)、求购买一个A商品和一个B商品各需要多少元;(2)、商店准备购买A、B两种商品共80个,若A 商品的数量不少于B商品数量的4倍,并且购买A、B商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?24. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D , 点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D , 分别交AC , AB于点E , F . (1)、试判断直线BC与⊙O的位置关系,并说明理由;(2)、若BD=2 ,BF=2,求阴影部分的面积(结果保留π).25. 如图
(1)、试判断直线BC与⊙O的位置关系,并说明理由;(2)、若BD=2 ,BF=2,求阴影部分的面积(结果保留π).25. 如图 (1)、阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
(1)、阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为;
(2)、问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.(3)、问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.26. 如图,已知抛物线 与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.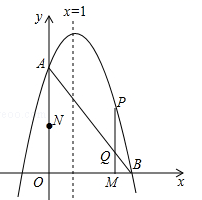 (1)、求此抛物线的解析式以及点B的坐标.(2)、动点M从点O出发,以每秒2个单位长度的速度沿x轴正方向运动,同时动点N从点O出发,以每秒3个单位长度的速度沿y轴正方向运动,当N点到达A点时,M、N同时停止运动.过动点M作x轴的垂线交线段AB于点Q,交抛物线于点P,设运动的时间为t秒.
(1)、求此抛物线的解析式以及点B的坐标.(2)、动点M从点O出发,以每秒2个单位长度的速度沿x轴正方向运动,同时动点N从点O出发,以每秒3个单位长度的速度沿y轴正方向运动,当N点到达A点时,M、N同时停止运动.过动点M作x轴的垂线交线段AB于点Q,交抛物线于点P,设运动的时间为t秒.①当t为何值时,四边形OMPN为矩形.
②当t>0时,△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.