湖南省常德市2020年中考数学二模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、-2 B、2 C、 D、2. 已知三角形中,某两条边的长分别为4和9则另一条边的长可能是( )A、4 B、5 C、12 D、133. 若函数 中,y的值随x值的增大而减小,则k的取值范围为( )A、 B、 C、 D、4. 若实数 在数轴上的对应点的位置如图所示,则正确的结论是( )
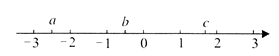 A、 B、 C、 D、5. 某班实行每周量化考核制,学期末对考核成绩进行统计,结果显示甲、乙两组的平均成绩相同,方差分别为 ,则两组成绩的稳定性是( )A、甲组比乙组的成绩稳定 B、乙组比甲组的成绩稳定 C、甲、乙两组的成绩一样稳定 D、无法确定6. 如图,矩形 中,O为 的中点,过点O作 分别交 于点 若 则 的长为( )
A、 B、 C、 D、5. 某班实行每周量化考核制,学期末对考核成绩进行统计,结果显示甲、乙两组的平均成绩相同,方差分别为 ,则两组成绩的稳定性是( )A、甲组比乙组的成绩稳定 B、乙组比甲组的成绩稳定 C、甲、乙两组的成绩一样稳定 D、无法确定6. 如图,矩形 中,O为 的中点,过点O作 分别交 于点 若 则 的长为( )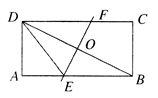 A、2 B、 C、 D、7. 下列计算错误的是( )A、 B、 C、 D、8. 已知实数 ,我们把 称为 的差倒数,如:-2的差倒数是 的差倒数是 .如果 是 的差倒数, 是 的差倒数, 是 的差倒数...依次类推,则 ( )A、48.5 B、49.5 C、50 D、51.5
A、2 B、 C、 D、7. 下列计算错误的是( )A、 B、 C、 D、8. 已知实数 ,我们把 称为 的差倒数,如:-2的差倒数是 的差倒数是 .如果 是 的差倒数, 是 的差倒数, 是 的差倒数...依次类推,则 ( )A、48.5 B、49.5 C、50 D、51.5二、填空题
-
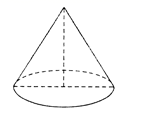
9. 的立方根是 .10. 一个多边形的内角和为1080°,则这个多边形是边形.11. 为防疫新冠病毒,我国的口罩产能大幅提升,今年四月初我国日产口罩达到 只,将 用科学记数法表示为 .12. 个正整数中,中位数是 ,唯一的众数是 则这 个数的和的最大值为 .13. 若关于x的一元二次方程 的一个根是-1,则另一个根是 .14. 如图,要用纸板制作一个母线长为 底面圆半径为 的圆锥形漏斗,若不计损耗,则所需纸板的面积是 .
 15. 将抛物线 向左平移1个单位,再向上平移3个单位,则平移后的抛物线的表达式为 .16. 如图,在 中,已知 依次连接 的三边中点, 得 ,再依次连接 的三边中点得 ,···,则 的周长为 .
15. 将抛物线 向左平移1个单位,再向上平移3个单位,则平移后的抛物线的表达式为 .16. 如图,在 中,已知 依次连接 的三边中点, 得 ,再依次连接 的三边中点得 ,···,则 的周长为 .
三、解答题
-
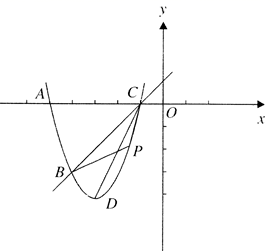
17. 计算: .18. 解不等式组:19. 先化简,再求值: ,其中 .20. 如图 的面积为 ,反比例函数 的图象经过点A
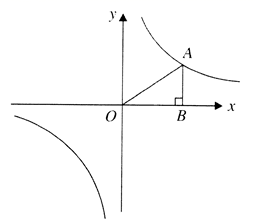 (1)、求反比例函数的解析式;(2)、从 四个点中任取两个点,请用树状图或列表法,求恰有一个点在反比例函数图象上的概率.21. 为鼓励学生参与体育锻炼,学校计划拿出不超过1600元的资金再购买一批篮球和排球.已知篮球和排球的单价比为 ,单价和为80元.(1)、篮球和排球的单价分别是多少元?(2)、若要求购买的篮球和排球的总数量是36个,且购买的篮球的数量多于25个,有哪几种购买方案?22. 如图, 是圆上的四个点, 的延长线相交于点D.
(1)、求反比例函数的解析式;(2)、从 四个点中任取两个点,请用树状图或列表法,求恰有一个点在反比例函数图象上的概率.21. 为鼓励学生参与体育锻炼,学校计划拿出不超过1600元的资金再购买一批篮球和排球.已知篮球和排球的单价比为 ,单价和为80元.(1)、篮球和排球的单价分别是多少元?(2)、若要求购买的篮球和排球的总数量是36个,且购买的篮球的数量多于25个,有哪几种购买方案?22. 如图, 是圆上的四个点, 的延长线相交于点D.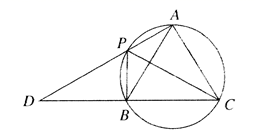 (1)、求证: 是等边三角形:(2)、若 ,求 的长.23. 某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据,整理绘制出下面的条形统计图:
(1)、求证: 是等边三角形:(2)、若 ,求 的长.23. 某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据,整理绘制出下面的条形统计图: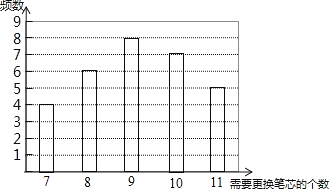
设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.
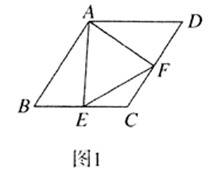
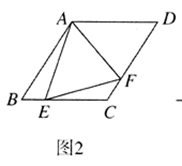
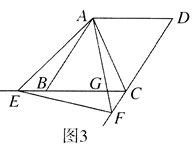
(1)、若n=9,求y与x的函数关系式;(2)、若要使这30支水彩笔“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5,确定n的最小值;(3)、假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯所需费用的平均数,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯.24. 在日常生活中,我们经常看到一些窗户上安装着遮阳篷,如图 ,现在要为一个面向正南的窗户设计安装一个遮阳篷,已知该地区冬天正午太阳最低时,光线与水平线的夹角为 ;夏天正午太阳最高时,光线与水平线的夹角为 .把图 画成图 ,其中 表示窗户的高, 表示直角形遮阳篷.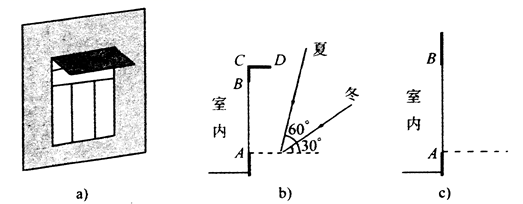 (1)、遮阳篷 怎样设计,才能正好在冬天正午太阳最低时光线最大限度地射入室内,而夏天正午太阳最高时光线刚好不射入室内?请在图 中画图表示;(2)、已知 ,在 的条件下,求出 的长度.
(1)、遮阳篷 怎样设计,才能正好在冬天正午太阳最低时光线最大限度地射入室内,而夏天正午太阳最高时光线刚好不射入室内?请在图 中画图表示;(2)、已知 ,在 的条件下,求出 的长度.