湖南省常德市澧县2020年中考数学模拟试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、单选题
-
1. 给出下列命题: ;(2)若 ,则x的相反数是2;(3) 的平方根是 ;(4) 是最简二次根式;(5) .其中正确命题的个数有( )A、5 B、4 C、3 D、22. 下列计算正确的是( )A、 B、 C、 D、3. 在中考体育加试中,某班30名男生的跳远成绩如下表:
成绩/m
1.95
2.00
2.05
2.10
2.15
2.25
人数
2
3
9
8
5
3
这些男生跳远成绩的众数、中位数分别是( )
A、2.10,2.05 B、2.10,2.10 C、2.05,2.10 D、2.05,2.054. 桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )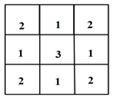 A、
A、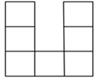 B、
B、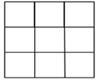 C、
C、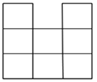 D、
D、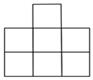 5. 如图,在 中,点D,E分别是 , 的中点, 与 交于点O,连接 .下列结论:(1) ;(2) ;(3) ;(4) .其中正确的个数有( )
5. 如图,在 中,点D,E分别是 , 的中点, 与 交于点O,连接 .下列结论:(1) ;(2) ;(3) ;(4) .其中正确的个数有( ) A、4 B、3 C、2 D、16. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则劣弧AC的长是( )
A、4 B、3 C、2 D、16. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则劣弧AC的长是( ) A、4π B、2π C、π D、7. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF.把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM.若矩形纸片的宽AB=4,则折痕BM的长为( )
A、4π B、2π C、π D、7. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF.把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM.若矩形纸片的宽AB=4,则折痕BM的长为( )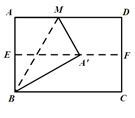 A、 B、 C、8 D、8. 对于一个函数,自变量x取a时,函数值y也等于a , 我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2 , 且x1<1<x2 , 则c的取值范围是( )A、c<﹣3 B、c<﹣2 C、c< D、c<1
A、 B、 C、8 D、8. 对于一个函数,自变量x取a时,函数值y也等于a , 我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2 , 且x1<1<x2 , 则c的取值范围是( )A、c<﹣3 B、c<﹣2 C、c< D、c<1二、填空题
-
9. 从 ,0, , ,3.5这五个数中随机抽取一个,则抽到无理数的概率为 .10. 某种冠状病毒的直径是120纳米,1纳米等于 米,则这种冠状病毒的直径(单位是米)用科学记数法表示为 .11. 分式 有意义时,x的取值范围是 .12. 方程 的解是 .13. 已知一次函数 的图象与正比例函数 的图象交于点 ,则关于 的不等式组 的解集为 .14. 已知圆锥的底面半径为2cm,侧面积为10πcm2 , 则该圆锥的母线长为cm.15. 如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE.若AB=2,∠ACB=30°,则线段CD的长度为.
 16. 如图,将从1开始的正整数按规律排列,例如:位于第3行、第4列的数是12,则位于第45行、第6列的数是 .
16. 如图,将从1开始的正整数按规律排列,例如:位于第3行、第4列的数是12,则位于第45行、第6列的数是 .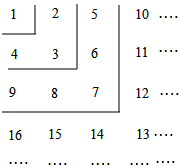
三、解答题
-
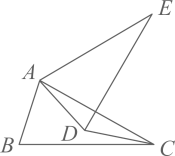
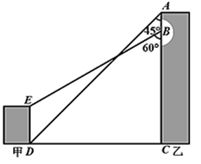
17. 计算:18. 解不等式组 ,并把不等式组的解集在数轴上表示出来19. 已知(1)、当 时,先化简A,再求A的值;(2)、代数式 的值能否等于3?请说明理由20. 如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为60°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据: , ,精确到0.1m.)
 21. 如图,在平面直角坐标系中,正六边形ABCDEF的对称中心P在反比例函数 的图象上,边CD在x轴上,点B在y轴上.已知 .
21. 如图,在平面直角坐标系中,正六边形ABCDEF的对称中心P在反比例函数 的图象上,边CD在x轴上,点B在y轴上.已知 .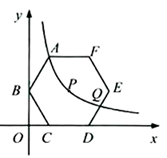 (1)、点A是否在该反比例函数的图象上?请说明理由.(2)、若该反比例函数图象与DE交于点Q,求点Q的横坐标.(3)、平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.22. 某超市用1200元购进一批甲玩具,用800元购进一批乙玩具,所购甲玩具件数是乙玩具件数的 ,已知甲玩具的进货单价比乙玩具的进货单价多1元.(1)、求:甲、乙玩具的进货单价各是多少元?(2)、玩具售完后,超市决定再次购进甲、乙玩具(甲、乙玩具的进货单价不变),购进乙玩具的件数比甲玩具件数的2倍多60件,求:该超市用不超过2100元最多可以采购甲玩具多少件?23. 为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
(1)、点A是否在该反比例函数的图象上?请说明理由.(2)、若该反比例函数图象与DE交于点Q,求点Q的横坐标.(3)、平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.22. 某超市用1200元购进一批甲玩具,用800元购进一批乙玩具,所购甲玩具件数是乙玩具件数的 ,已知甲玩具的进货单价比乙玩具的进货单价多1元.(1)、求:甲、乙玩具的进货单价各是多少元?(2)、玩具售完后,超市决定再次购进甲、乙玩具(甲、乙玩具的进货单价不变),购进乙玩具的件数比甲玩具件数的2倍多60件,求:该超市用不超过2100元最多可以采购甲玩具多少件?23. 为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题: (1)、本次抽样调查测试的建档立卡贫困户的总户数.(2)、图1中,∠α的度数是 , 并把图2条形统计图补充完整.(3)、某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?(4)、调查人员想从5户建档立卡贫困户(分别记为 )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户 的概率.24. 如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.
(1)、本次抽样调查测试的建档立卡贫困户的总户数.(2)、图1中,∠α的度数是 , 并把图2条形统计图补充完整.(3)、某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?(4)、调查人员想从5户建档立卡贫困户(分别记为 )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户 的概率.24. 如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.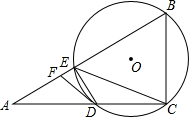 (1)、求证:DF是⊙O的切线.(2)、若D是AC的中点,∠A=30°,BC=4,求DF的长.25. 如图
(1)、求证:DF是⊙O的切线.(2)、若D是AC的中点,∠A=30°,BC=4,求DF的长.25. 如图 (1)、(探究证明)
(1)、(探究证明)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图①,在矩形ABCD中,EF⊥GH , EF分别交AB , CD于点E , F , GH分别交AD , BC于点G , H.求证: ;
(2)、如图②,在满足(1)的条件下,又AM⊥BN , 点M , N分别在边BC , CD上,若 ,则 的值为;(3)、(联系拓展)如图③,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN , 点M , N分别在边BC , AB上,求 的值.
26. 如图1,在平面直角坐标系中,一次函数y=﹣ x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.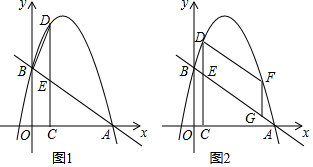 (1)、求抛物线的函数表达式(2)、是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;(3)、如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.
(1)、求抛物线的函数表达式(2)、是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;(3)、如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.