浙江省温州乐清市2020年数学中考适应性卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. 计算: ( )A、-1 B、1 C、4 D、-42. 天文单位是天文学中计量天体之间距离的一种单位,其数值取地球与太阳之间的平均距离,即149597870700m,约为149600000km.将数149600000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算中,正确的是( )A、 B、 C、 D、4. 在一个不透明袋子中装有 个只有颜色不同的球,其中3个红球和4个蓝球,从袋子中任意摸出1个球,是红球的概率为( )A、 B、 C、 D、5. 某校九年级(1)班体育委员对本班50名同学参加球类项目做了统计(每人选一种),绘制成如图所示统计图,则该班参加乒乓球和羽毛球项目的人数总和为( )
 A、20人 B、25人 C、30人 D、35人6. 公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即: 阻力 阻力臂=动力 动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是 和 ,则动力F (单位: N)关于动力臂L(单位: )的函数解析式正确的是( )A、 B、 C、 D、7. 如图,某地修建高速公路,要从 地向 地修一条隧道(点 在同一水平面上).为了测量 两地之间的距离,一架直升飞机从 地出发,垂直上升800米到达C处,在C处观察B地的俯角 为 ,则 两地之间的距离为( )
A、20人 B、25人 C、30人 D、35人6. 公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即: 阻力 阻力臂=动力 动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是 和 ,则动力F (单位: N)关于动力臂L(单位: )的函数解析式正确的是( )A、 B、 C、 D、7. 如图,某地修建高速公路,要从 地向 地修一条隧道(点 在同一水平面上).为了测量 两地之间的距离,一架直升飞机从 地出发,垂直上升800米到达C处,在C处观察B地的俯角 为 ,则 两地之间的距离为( ) A、 米 B、 米 C、 米 D、 米8. 若扇形的弧长是 ,半径是18,则该扇形的圆心角是( )A、 B、 C、 D、9. 已知抛物线 的对称轴为直线 ,记 ,则下列选项中一定成立的是( )A、 B、 C、 D、10. 如图,在矩形 中,E为 中点,以 为边作正方形 ,边 交 于点H,在边 上取点M使 ,作 交 于点L,交 于点N,欧几里得在《几何原本》中利用该图解释了 ,现以点 为圆心, 为半径作圆弧交线段 于点P,连结 ,记 的面积为 ,图中阴影部分的面积为 .若点A,L,G在同一直线上,则 的值为( )
A、 米 B、 米 C、 米 D、 米8. 若扇形的弧长是 ,半径是18,则该扇形的圆心角是( )A、 B、 C、 D、9. 已知抛物线 的对称轴为直线 ,记 ,则下列选项中一定成立的是( )A、 B、 C、 D、10. 如图,在矩形 中,E为 中点,以 为边作正方形 ,边 交 于点H,在边 上取点M使 ,作 交 于点L,交 于点N,欧几里得在《几何原本》中利用该图解释了 ,现以点 为圆心, 为半径作圆弧交线段 于点P,连结 ,记 的面积为 ,图中阴影部分的面积为 .若点A,L,G在同一直线上,则 的值为( )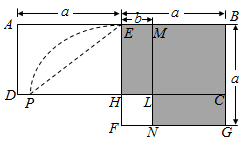 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 不等式组 的解集是.13. 某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.8,最后一组的频数是10,则此次抽样调查的人数为 人. (注: 横轴上每组数据包含最小值不包含最大值)
 14. 如图, 是 上的四点,点B为 的中点, 过点 ,那么 度.
14. 如图, 是 上的四点,点B为 的中点, 过点 ,那么 度. 15. 如图,在 中, ,作 关于直线 的轴对称图形 点 是 的中点,若点 在同一直线上,则 的长为.
15. 如图,在 中, ,作 关于直线 的轴对称图形 点 是 的中点,若点 在同一直线上,则 的长为. 16. 由四个正方形相框拼成的照片墙如图所示,已知正方形 ,正方形 ,正方形 的.面积分别为4平方分米,4平方分米, 平方分米,则正方形 的面积为平方分米.
16. 由四个正方形相框拼成的照片墙如图所示,已知正方形 ,正方形 ,正方形 的.面积分别为4平方分米,4平方分米, 平方分米,则正方形 的面积为平方分米.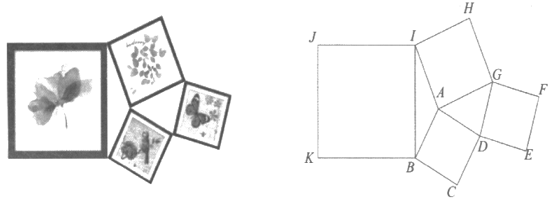
三、解答题
-
17.(1)、计算:(2)、化简:18. 如图,在 中, 的平分线 相交于点E,过点E作 交 于点G,交 的延长线于点D
 (1)、求证:(2)、当 时,求 的长.19. 如图,点 是 的方格纸中的三个格点,按下列要求作出格点四边形(顶点在格点上).(1)、在图1中画出一个以A,C为顶点的菱形,使点B在该图形内部(不包括在边界上).
(1)、求证:(2)、当 时,求 的长.19. 如图,点 是 的方格纸中的三个格点,按下列要求作出格点四边形(顶点在格点上).(1)、在图1中画出一个以A,C为顶点的菱形,使点B在该图形内部(不包括在边界上).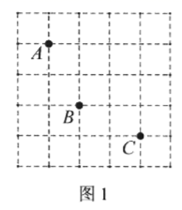 (2)、在图2中画出一个以A,C为顶点的平行四边形,使该图形的一边所在直线与 夹角为
(2)、在图2中画出一个以A,C为顶点的平行四边形,使该图形的一边所在直线与 夹角为 20. 某公司销售部有营业员 人,某一月的销售量统计如下表所示:
20. 某公司销售部有营业员 人,某一月的销售量统计如下表所示:公司 名营业员某一月的销售量统计表
月销售量/件数
1770
480
220
180
120
90
人数
1
1
3
3
3
4
(1)、求这 名营业员该月销售量数据的平均数;(2)、这 名营业员该月销售量数据的中位数是 件,众数是件,为了提高大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择.确定“定额”的统计量为(填“中位数”或“众数”)21. 如图,在平面直角坐标系中,点 是一次函数 图象上两点,它们的横坐标分别为 其中 ,过点 分别作 轴的平行线,交抛物线 于点 , (1)、若 求a的值;(2)、点E是抛物线上的一点,求 面积的最小值.22. 如图,在 中,以 为直径的 交 边于点 ,过点 作 于点 ,交 于点 ,连结
(1)、若 求a的值;(2)、点E是抛物线上的一点,求 面积的最小值.22. 如图,在 中,以 为直径的 交 边于点 ,过点 作 于点 ,交 于点 ,连结 (1)、求证:(2)、当 时,求 的直径.23. 某单位计划购进 三种型号的礼品共2700件,其中C型号礼品500件,A型号礼品比 型号礼品多200件.已知三种型号礼品的单价如下表:
(1)、求证:(2)、当 时,求 的直径.23. 某单位计划购进 三种型号的礼品共2700件,其中C型号礼品500件,A型号礼品比 型号礼品多200件.已知三种型号礼品的单价如下表:型号
A
B
C
单价(元/件)
30
20
10
(1)、求计划购进A和B两种型号礼品分别多少件?(2)、实际购买时,厂家给予打折优惠销售(如: 折指原价 ,在计划总价额不变的情况下,准备购进这批礼品.①若只购进 两种型号礼品,且 型礼品件数不超过C型礼品的 倍,求 型礼品最多购进多少件?
②若只购进 两种型号礼品,它们的单价分别打a折、b折, 均为整数,且购进的礼品总数比计划多300件,求 的值.
24. 如图1, 内接于 分别是 和 所对弧的中点,弦 分别交 于点 ,连结
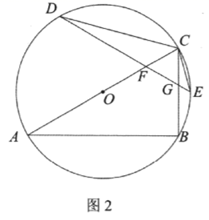
 (1)、求证: 是等边三角形.(2)、若
(1)、求证: 是等边三角形.(2)、若①如图2,当 为 的直径时,求 的长.
②当 将 的面积分成了 的两部分时,求 的长.
(3)、连结 交 于点H,若 :则 的值为. (请直接写出答案)