浙江省宁波市海曙区2020年数学中考模拟试卷（5月）

试卷更新日期：2020-07-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 如图所示，点M表示的数是（）

A、2.5 B、﹣1.5 C、﹣2.5 D、1.5

查看试题解析
2. 在单词“NAME”的四个字母中，轴对称图形有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3.
如图，是由相同小正方体组成的立体图形，它的主视图为（）

A、 B、 C、 D、

查看试题解析
4. 老师要分析小刚的5次数学模拟考试成绩是否稳定，她需要统计小刚这5次成绩的（）

A、平均数 B、方差或标准差 C、众数 D、中位数

查看试题解析
5. 已知代数式x²+3x+5的值为7，那么代数式3x²+9x﹣2的值是（）

A、0 B、2 C、4 D、6

查看试题解析
6. 如图，AB为⊙O的直径，AB＝30，点C在⊙O上，∠A＝24°，则 $\overset{⌢}{AC}$ 的长为（）

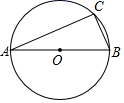A、9π B、10π C、11π D、12π

查看试题解析
7. 小明用四根长度相同的木条首尾相接制作了能够活动的学具，他先活动学具成为图1所示，并测得∠B＝60°，接着活动学具成为图2所示，并测得∠ABC＝90°，若图2对角线BD＝40cm，则图1中对角线BD的长为（）

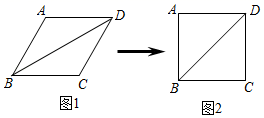A、20cm B、20 $\sqrt{2}$ cm C、20 $\sqrt{3}$ cm D、20 $\sqrt{6}$ cm

查看试题解析
8. 已知分式 $\frac{- 6 x + b}{x + a}$ （a，b为常数）满足下列表格中的信息：则下列结论中错误的是（）

x的取值

﹣1

1

c

d

分式的值

无意义

1

0

﹣1

A、a＝1 B、b＝8 C、c＝ $\frac{4}{3}$ D、d＝ $\frac{7}{6}$

查看试题解析
9. 下列3个图形中，阴影部分的面积为1的个数为（）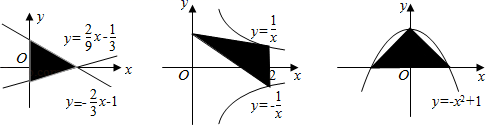

A、3个 B、2个 C、1个 D、0个

查看试题解析
10. 如图，矩形ABCD中，E为边AD上一点（不为端点），EF⊥AD交AC于点F，要求△FBC的面积，只需知道下列哪个三角形的面积即可（）

A、△EBC B、△EBF C、△ECD D、△EFC

查看试题解析

二、填空题

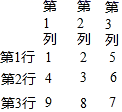
11. 计算（a+b）²＝.

查看试题解析
12. 从正三角形、正方形、正五边形、圆这四个图形中随机选出一个图形，结果是中心对称图形的概率为.

查看试题解析
13. 把所有的正整数按一定规律排列成如图所示的数表，若根据行列分布，正整数6对应的位置记为（2，3），则位置（4，2）对应的正整数是.

查看试题解析
14. 如图，在△ABC中，∠ACB为钝角，把边AC绕点A沿逆时针方向旋转90°得AD，把边BC绕点B沿顺时针方向旋转90°得BE，作DM⊥AB于点M，EN⊥AB于点N，若AB＝5，EN＝2，则DM＝.

查看试题解析
15. 已知二次函数y＝ax²﹣2ax+c（a＜0）图象上的两点（x₁ ， y₁）和（3，y₂），若y₁＞y₂ ，则x₁的取值范围是.

查看试题解析
16. 如图，已知△ABC中，∠ACB＝90°，D是斜边AB上一点，BD＝2AD，CD＝4，则S_△_ACD的最大值为.

查看试题解析

三、解答题

17.

(1)、已知|a+2|+ $\sqrt{b - 3}$ ＝0，求a^b.

(2)、先化简，再求值： $(\frac{3 x}{x - 1} - \frac{x}{x + 1}) \cdot \frac{x^{2} - 1}{x}$ ，其中x＝ $\sqrt{2}$ ﹣2.

查看试题解析
18. 如图，△ABC中，∠C＝90°，AC＝3x﹣10.

(1)、已知AC＞2，求x的取值范围；

(2)、若AB＝x+2，且x为整数，在（1）的条件下，求BC的长.

查看试题解析
19. 如图，在平面直角坐标系中，B（5，0），点A在第一象限，且OA＝OB，sin∠AOB＝ $\frac{3}{5}$ .

(1)、求过点O，A，B三点的抛物线的解析式.

(2)、若y＝ $\frac{k}{x}$ 的图象过（1）中的抛物线的顶点，求k的值.

查看试题解析

20. 某校兴趣小组以问卷调查的形式，随机调查了某地居民对武汉封城后续措施的了解情况，设置了多选题，并将调查结果绘制成如图不完整的统计图.

选项	A	B	C	D	E
后续措施	扩大宣传力度	分类隔离病人	封闭小区	聘请专业物资	采取其他措施
选择人次	25		85	15	35

已知平均每人恰好选择了两个选项，根据以上信息回答下列问题：

(1)、求参与本次问卷调查的居民人数，并补全条形统计图；

(2)、在扇形统计图中，求E选项对应圆心角α的度数；

(3)、根据此次调查结果估计该地100万居民当中选择D选项的人数.

查看试题解析

21. 如图，△ABC内接于⊙O，AB＝AC，过A作AP∥BC交CO的延长线于点P.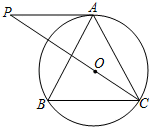

(1)、求证：PA是⊙O的切线；

(2)、若BC＝8，tanB＝2，求PA的长.

查看试题解析
22. 如图1是两圆柱形连通容器，两根铁棒直立于甲容器底部（连通处及铁棒体积忽略不计），向甲容器匀速注水，甲容器的水面高度h（cm）与时间t（分）的函数关系如图2所示.已知两根铁棒的长度之和为34cm，当水面达到连通处时，一根露出水面的长度是它的 $\frac{1}{3}$ ，另一根露出水面的长度是它的 $\frac{1}{4}$ .

(1)、①图2中（3，a）表示的实际意义是 ▲ ；
②请求出a的值；

(2)、若甲、乙两容器的底面积之比为S_甲， S_乙＝3：2.
①直接写出b的值为 ▲ ；

②求点P的坐标.

查看试题解析
23. 定义：有一组邻边均和一条对角线相等的四边形叫做邻和四边形.

(1)、如图1，四边形ABCD中，∠ABC＝70°，∠BAC＝40°，∠ACD＝∠ADC＝80°，求证：四边形ABCD是邻和四边形.

(2)、如图2，是由50个小正三角形组成的网格，每个小正三角形的顶点称为格点，已知A，B，C三点的位置如图，请在网格图中标出所有的格点D，使得以A，B，C，D为顶点的四边形为邻和四边形.

(3)、如图3，△ABC中，∠ABC＝90°，AB＝4，BC＝4 $\sqrt{3}$ ，若存在一点D，使四边形ABCD是邻和四边形，求邻和四边形ABCD的面积.

查看试题解析
24. 如图1，△ABC内接于圆，点D在劣弧 $\overset{⌢}{AC}$ 上，AD＝ $\frac{1}{2}$ BC，DC＝ $\frac{1}{2}$ AB，Q为AC中点，点D与点P关于点Q对称.

(1)、求证：△PAD∽△ABC.

(2)、求证：点B，P，D在一条直线上.

(3)、如图2，记∠PAB＝α，∠PCB＝β，∠ABC＝θ，请用含α，β的代数式表示θ.

(4)、如图3，设E，F分别为AB，BC的中点，EF交BD于点H，求 $\frac{P H}{A C}$ 的值.

查看试题解析

x的取值	﹣1	1	c	d
分式的值	无意义	1	0	﹣1