云南省曲靖市马龙区2020年数学中考一模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. 曲靖市的职业教育是曲靖市教育的一张名片,现在曲靖市中等职业学校在校生约为130000人,将数字130000用科学记数法表示为( )A、0.13×105 B、0.13×106 C、1.3×105 D、1.3×1062. 下列计算正确的是( )A、a2+a2=a4 B、a2•a3=a6 C、(﹣a2)2=a4 D、(a+1)2=a2+13. 如图,在下面的四个几何体中,从它们各自的正面和左面看,不相同的是( )A、
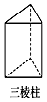 B、
B、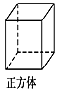 C、
C、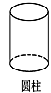 D、
D、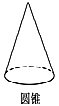 4. 已知反比例函数y= 的图象上有两点A(x1 , y1),B(x2 , y2),当x1<0<x2时,有y1<y2 , 则m的取值范围是( )A、m<0 B、m>0 C、m< D、m>5. 为了参加市中学生篮球运动会,一支校篮球队准备购买10双运动鞋,各种尺码统计如下表:
4. 已知反比例函数y= 的图象上有两点A(x1 , y1),B(x2 , y2),当x1<0<x2时,有y1<y2 , 则m的取值范围是( )A、m<0 B、m>0 C、m< D、m>5. 为了参加市中学生篮球运动会,一支校篮球队准备购买10双运动鞋,各种尺码统计如下表:尺码(厘米)
25
25.5
26
26.5
27
购买量(双)
1
2
3
2
2
则这10双运动鞋尺码的众数和中位数分别为( )
A、25.5厘米,26厘米 B、26厘米,25.5厘米 C、25.5厘米,25.5厘米 D、26厘米,26厘米6. 如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则FC为( )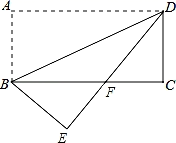 A、 B、 C、2 D、37. 如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=( )
A、 B、 C、2 D、37. 如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=( ) A、2 B、 C、 D、8. 如图,在△ABC中,AB=4,若将ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD则点A的运动路径AB与线段AD、A′D围成的阴影部分的面积是( )
A、2 B、 C、 D、8. 如图,在△ABC中,AB=4,若将ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD则点A的运动路径AB与线段AD、A′D围成的阴影部分的面积是( )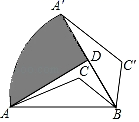 A、 ﹣2 B、 ﹣4 C、 ﹣2 D、 ﹣4
A、 ﹣2 B、 ﹣4 C、 ﹣2 D、 ﹣4二、填空题
-
9. ﹣ 的相反数是 , 倒数是 , 绝对值是 .10. 不等式组 的解集为.11. 如图,AB∥CD,FE⊥DB,垂足为点E,∠2=40°,则∠1的度数是.
 12. 关于x的方程mx2﹣4x+1=0有实数根,则m的取值范围是.13. 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为.
12. 关于x的方程mx2﹣4x+1=0有实数根,则m的取值范围是.13. 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为. 14. 如图,每个图案都由若干个棋子摆成,按照此规律,第n个图案中棋子的总个数可用含n的代数式表示为.
14. 如图,每个图案都由若干个棋子摆成,按照此规律,第n个图案中棋子的总个数可用含n的代数式表示为.
三、解答题
-
15. 计算: .16. 先化简,再求值: ,其中 .17. 如图,四边形ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F、G.求证:AF=DG
 18. 某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图所示.已知:洗衣机的排水速度为每分钟20升.
18. 某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图所示.已知:洗衣机的排水速度为每分钟20升.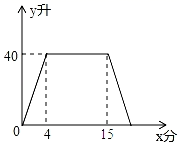 (1)、求排水时y与x之间的函数解析式;(2)、洗衣机中的水量到达某一水位后,过13.7分钟又到达该水位,求该水位为多少升.19. 曲靖市某街道学苑社区开展爱心捐赠活动,并决定赠送一批阅读图书,用于贫困学生的课外学习.据了解,科普书的单价比文学书的单价多8元,用12000元购买科普书与用8000元购买文学书的本数相同,求这两类书籍的单价各是多少元.20. 已知,如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)、求排水时y与x之间的函数解析式;(2)、洗衣机中的水量到达某一水位后,过13.7分钟又到达该水位,求该水位为多少升.19. 曲靖市某街道学苑社区开展爱心捐赠活动,并决定赠送一批阅读图书,用于贫困学生的课外学习.据了解,科普书的单价比文学书的单价多8元,用12000元购买科普书与用8000元购买文学书的本数相同,求这两类书籍的单价各是多少元.20. 已知,如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.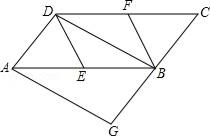 (1)、求证:四边形AGBD为平行四边形;(2)、若四边形AGBD是矩形,则四边形BEDF是什么特殊四边形?证明你的结论.21. 某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)、求证:四边形AGBD为平行四边形;(2)、若四边形AGBD是矩形,则四边形BEDF是什么特殊四边形?证明你的结论.21. 某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题: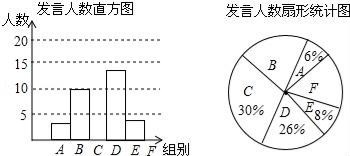 (1)、求样本容量,并补全直方图;(2)、该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;(3)、已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
(1)、求样本容量,并补全直方图;(2)、该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;(3)、已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.发言次数n
A
0≤n<3
B
3≤n<6
C
6≤n<9
D
9≤n<12
E
12≤n<15
F
15≤n<18
22. 如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G,且∠ABG=2∠C.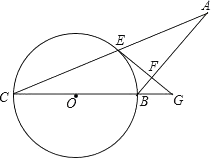 (1)、求证:EG是⊙O的切线;(2)、若tanC= ,AC=8,求⊙O的半径.
(1)、求证:EG是⊙O的切线;(2)、若tanC= ,AC=8,求⊙O的半径.
23. 如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的交点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.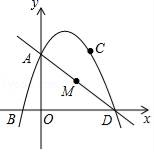 (1)、求抛物线的表达式;(2)、过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)(3)、在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;(4)、在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.
(1)、求抛物线的表达式;(2)、过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)(3)、在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;(4)、在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.