陕西省宝鸡市凤翔县2020年数学中考一模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
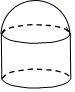
1. 在实数 中,最小的数是( )A、0 B、-2 C、 D、2. 一个由半球和圆柱组成的几何体如图水平放置,其俯视图为( )
 A、
A、 B、
B、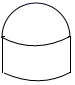 C、
C、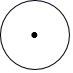 D、
D、 3. 如图所示, 垂足为 则 的度数为( )
3. 如图所示, 垂足为 则 的度数为( )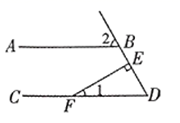 A、 B、 C、 D、4. 下列计算正确的是( )A、(﹣2a)3=﹣2a3 B、(﹣a)2•(﹣a)3=a6 C、(a+b)2=a2+b2 D、(a+b)(a﹣b)=a2﹣b25. 已知一个正比例函数的图象经过 和 两点,则 间的关系一定是( )A、 B、 C、 D、6. 如图,在 中,∠C=90°,D为AC上一点,若DA=DB=15,△ABD的面积为90,则CD的长是( )
A、 B、 C、 D、4. 下列计算正确的是( )A、(﹣2a)3=﹣2a3 B、(﹣a)2•(﹣a)3=a6 C、(a+b)2=a2+b2 D、(a+b)(a﹣b)=a2﹣b25. 已知一个正比例函数的图象经过 和 两点,则 间的关系一定是( )A、 B、 C、 D、6. 如图,在 中,∠C=90°,D为AC上一点,若DA=DB=15,△ABD的面积为90,则CD的长是( )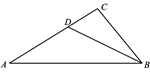 A、6 B、9 C、12 D、7. 若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,﹣1),B(1,1),则不等式kx+b>1的解集为( )A、x<1 B、x>1 C、x>0 D、x<08. 如图,在矩形 中,点E在 上,连接 则 的周长等于( )
A、6 B、9 C、12 D、7. 若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,﹣1),B(1,1),则不等式kx+b>1的解集为( )A、x<1 B、x>1 C、x>0 D、x<08. 如图,在矩形 中,点E在 上,连接 则 的周长等于( ) A、6 B、 C、 D、9. 已知OA,OB是圆O的半径,点C,D在圆O上,且OA∥BC,若∠ADC=26°,则∠B的度数为( )
A、6 B、 C、 D、9. 已知OA,OB是圆O的半径,点C,D在圆O上,且OA∥BC,若∠ADC=26°,则∠B的度数为( )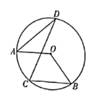 A、30° B、42° C、46° D、52°10. 在平面直角坐标系中,有两条抛物线关于 x 轴对称,且它们的顶点相距 6 个单位长度,若其中一条抛物线的函数表达式为 y=﹣x2+4x+m,则 m 的值是( )A、1 或 7 B、﹣1 或 7 C、1 或﹣7 D、﹣1 或-7
A、30° B、42° C、46° D、52°10. 在平面直角坐标系中,有两条抛物线关于 x 轴对称,且它们的顶点相距 6 个单位长度,若其中一条抛物线的函数表达式为 y=﹣x2+4x+m,则 m 的值是( )A、1 或 7 B、﹣1 或 7 C、1 或﹣7 D、﹣1 或-7二、填空题
-
11. 4是的算术平方根.12. 若某正六边形的边长是 则该正六边形的边心距为.13. 如图,已知正方形 的边长为 点 分别在 轴的正半轴上, 与反比例函数 的图象在第一象限的部分相交于点 若 则 .
 14. 如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,AE+CF=4,则△BEF面积的最小值为.
14. 如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,AE+CF=4,则△BEF面积的最小值为.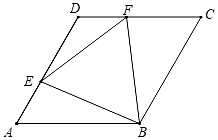
三、解答题
-
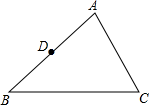
15. 计算: .16. 解方程: .17. 如图,已知△ABC中,D为AB的中点,请在边AC作点E,使得DE= BC(保留作图痕迹,不要求写作法)
 18. 如图,AB=AC, , 求证:BD=CE.
18. 如图,AB=AC, , 求证:BD=CE.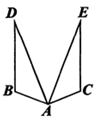 19. 2020年3月24日,工信部发布《关于推动 加快发展的通知》,全力推进 网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向 迁移,推动“ 医疗健康”创新发展,实施“ 工业互联网”512工程,促进“ 车联网”协同发展,构建 应用生态系统.现“ 网络”已成为一个热门词汇,某校为了解九年级学生对“ 网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
19. 2020年3月24日,工信部发布《关于推动 加快发展的通知》,全力推进 网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向 迁移,推动“ 医疗健康”创新发展,实施“ 工业互联网”512工程,促进“ 车联网”协同发展,构建 应用生态系统.现“ 网络”已成为一个热门词汇,某校为了解九年级学生对“ 网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题: (1)、请补全条形统计图,扇形统计图中 ▲_;(2)、所调查学生成绩的众数是 分,平均数是 _分;(3)、若该校九年级学生有 人,请估计得分不少于 分的有多少人?20. 某公园有一座古塔,古塔前有一个斜坡 坡角 ,斜坡高 米, 平行于水平地面 的一个平台.小华想利用所学知识测量古塔的高度 她在平台的点 处水平放置--平面镜,并沿着 方向移动,当移动到点N时,刚好在镜面中看到古塔顶端点 的像,这时,测得小华眼睛与地面的距离 米, 米, 米, 米,已知 请你根据题中提供的相关信息,求出古塔的高度 .(参考数据: )
(1)、请补全条形统计图,扇形统计图中 ▲_;(2)、所调查学生成绩的众数是 分,平均数是 _分;(3)、若该校九年级学生有 人,请估计得分不少于 分的有多少人?20. 某公园有一座古塔,古塔前有一个斜坡 坡角 ,斜坡高 米, 平行于水平地面 的一个平台.小华想利用所学知识测量古塔的高度 她在平台的点 处水平放置--平面镜,并沿着 方向移动,当移动到点N时,刚好在镜面中看到古塔顶端点 的像,这时,测得小华眼睛与地面的距离 米, 米, 米, 米,已知 请你根据题中提供的相关信息,求出古塔的高度 .(参考数据: ) 21. 对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间是一次函数关系.如图所示是一个家用温度表的表盘、其左边为摄氏温度的刻度和读数(单位 ),右边为华氏温度的刻度和读数(单位 ).从温度计的刻度上可以看出,摄氏温度 与华氏温度 部分对应关系如下表:
21. 对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间是一次函数关系.如图所示是一个家用温度表的表盘、其左边为摄氏温度的刻度和读数(单位 ),右边为华氏温度的刻度和读数(单位 ).从温度计的刻度上可以看出,摄氏温度 与华氏温度 部分对应关系如下表:···
-40
50
···
···
−40
122
···
 (1)、求y与x之间的函数关系式;(2)、当摄氏温度为零下 时,求华氏温度为多少?22. 自2020年初新冠肺炎疫情爆发以来,国内经济--度被按下暂停键,如今随着国内疫情防控形势持续向好,各地开始进入积极复工复产的新模式.某商家为降低疫情带来的影响,刺激消费,吸引顾客,特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两个转盘的指针所指字母相同时,消费者就可以获得一次八折优惠价购买商品的机会.
(1)、求y与x之间的函数关系式;(2)、当摄氏温度为零下 时,求华氏温度为多少?22. 自2020年初新冠肺炎疫情爆发以来,国内经济--度被按下暂停键,如今随着国内疫情防控形势持续向好,各地开始进入积极复工复产的新模式.某商家为降低疫情带来的影响,刺激消费,吸引顾客,特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两个转盘的指针所指字母相同时,消费者就可以获得一次八折优惠价购买商品的机会.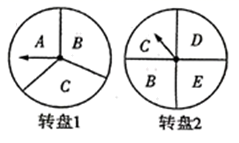 (1)、用树状图或列表的方法表示出游戏可能出现的所有结果;(2)、若小亮参加一次游戏,则他能获得八折优惠价购买商品的概率是多少?23. 如图,在等腰△ABC中,AC=BC,以BC为直径的⊙O与底边AB交于点D,过D作⊙O的切线交AC于点E.
(1)、用树状图或列表的方法表示出游戏可能出现的所有结果;(2)、若小亮参加一次游戏,则他能获得八折优惠价购买商品的概率是多少?23. 如图,在等腰△ABC中,AC=BC,以BC为直径的⊙O与底边AB交于点D,过D作⊙O的切线交AC于点E.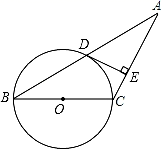 (1)、证明:DE⊥AC.(2)、若BC=8,AD=6,求AE的长.24. 如图,在平面直角坐标系中,顶点为M的抛物线C₁:y=ax2+bx与x轴的另一个交点为A(2,0),连接OM、AM,∠OMA=90°.
(1)、证明:DE⊥AC.(2)、若BC=8,AD=6,求AE的长.24. 如图,在平面直角坐标系中,顶点为M的抛物线C₁:y=ax2+bx与x轴的另一个交点为A(2,0),连接OM、AM,∠OMA=90°.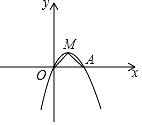 (1)、求抛物线C1的函数表达式;(2)、已知点D的坐标为(0,﹣2),将抛物线C1向上平移得到抛物线C2 , 抛物线C2与x轴分别交于点E、F(点E在点F的左侧),如果△DOM与△MAF相似,求所有符合条件的抛物线C2的函数表达式.25.(1)、问题提出:如图①在 中, 是 边 的高,点E是 上任意一点,若 则 的最小值为_;
(1)、求抛物线C1的函数表达式;(2)、已知点D的坐标为(0,﹣2),将抛物线C1向上平移得到抛物线C2 , 抛物线C2与x轴分别交于点E、F(点E在点F的左侧),如果△DOM与△MAF相似,求所有符合条件的抛物线C2的函数表达式.25.(1)、问题提出:如图①在 中, 是 边 的高,点E是 上任意一点,若 则 的最小值为_;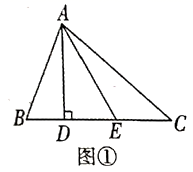 (2)、如图②,在等腰 中, 是 的垂直平分线,分别交 于点 , ,求 的周长;
(2)、如图②,在等腰 中, 是 的垂直平分线,分别交 于点 , ,求 的周长;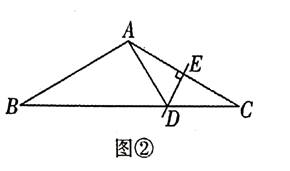 (3)、问题解决:
(3)、问题解决:如图③,某公园管理员拟在园内规划一个 区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路 和 ,满足 点 到 的距离为 .为了节约成本,要使得 之和最短,试求 的最小值(路宽忽略不计).