宁夏中卫市中宁县2020年数学中考二模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. 下列各式正确的是( )A、6a2﹣5a2=a2 B、(2a)2=2a2 C、﹣2(a﹣1)=﹣2a+1 D、(a+b)2=a2+b22. 一组数据:5,7,10,5,7,5,6,这组数据的众数和中位数分别是( )A、10和7 B、5和7 C、6和7 D、5和63. 中宁县位于宁夏回族自治区中部西侧,是世界枸杞的发源地和正宗原产地,已有600多年的历史.1995年被国务院命名为“中国枸杞之乡”; 将“中国枸杞之乡”六个字分别写在一个正方体的六个面上,这个正方体的展开图如图所示,那么在这个正方体中,和“杞”字相对的字是( )
 A、中 B、国 C、枸 D、乡4. 某公司2020年3月份营业额为60万元,5月份营业额达到100万元,设该公司这两个月的月平均增长率为x.应列方程是( )A、60(1+x)=100 B、60(1+x)2=100 C、60(1+x)+60(1+x)2=100 D、60+60(1+x)+60(1+x)2=1005. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、6. 如图,点A、点B是函数y= 的图象上关于坐标原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积是4,则k的值是( )
A、中 B、国 C、枸 D、乡4. 某公司2020年3月份营业额为60万元,5月份营业额达到100万元,设该公司这两个月的月平均增长率为x.应列方程是( )A、60(1+x)=100 B、60(1+x)2=100 C、60(1+x)+60(1+x)2=100 D、60+60(1+x)+60(1+x)2=1005. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、6. 如图,点A、点B是函数y= 的图象上关于坐标原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积是4,则k的值是( )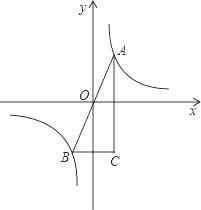 A、-2 B、±4 C、2 D、±27. 如图⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数为( )
A、-2 B、±4 C、2 D、±27. 如图⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数为( )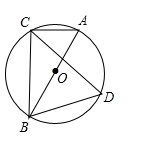 A、30° B、45° C、60° D、75°8. a≠0,函数y= 与y=﹣ax2+a在同一直角坐标系中的大致图象可能是( )A、
A、30° B、45° C、60° D、75°8. a≠0,函数y= 与y=﹣ax2+a在同一直角坐标系中的大致图象可能是( )A、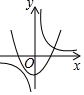 B、
B、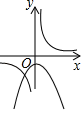 C、
C、 D、
D、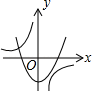
二、填空题
-
9. 分解因式:x3y﹣2x2y+xy= .10. 已知有理数 在数轴上的位置如图所示,则化简 的结果为.
 11. 一个不透明的口袋中装有5个红球和若干个白球,他们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,估计口袋中白球有个.12. 已知 ,则 的值为.13. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,∠EFB=60°,则AB的长是.
11. 一个不透明的口袋中装有5个红球和若干个白球,他们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,估计口袋中白球有个.12. 已知 ,则 的值为.13. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,∠EFB=60°,则AB的长是.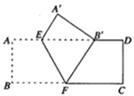 14. 如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连结CD.若CD=AC,∠A=48°,则∠ACB= .
14. 如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连结CD.若CD=AC,∠A=48°,则∠ACB= .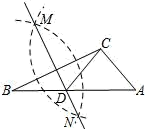 15. 如图,港口A在观测站O的正东方向,OA=6,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为.
15. 如图,港口A在观测站O的正东方向,OA=6,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为.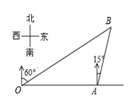 16. 如图,一块含有 角的直角三角板 ,在水平桌面上绕点C按顺时针方向旋转到 的位置,若 ,那么顶点A从开始到结束所经过的路径长为.(结果保留π)
16. 如图,一块含有 角的直角三角板 ,在水平桌面上绕点C按顺时针方向旋转到 的位置,若 ,那么顶点A从开始到结束所经过的路径长为.(结果保留π)
三、解答题
-
17. 先化简,再求值: ,其中, .18. 解不等式组: .19. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
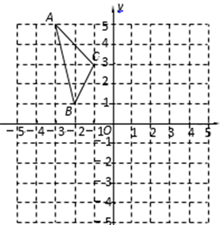
①画出△ABC关于y轴的对称图形△A1B1C1;
②画出△A1B1C1向右平移1个单位,向下平移5个单位长度后得到的△A2B2C2.
20. 近些年来,“校园安全”受到全社会的广泛关注,为了了解学生对于安全知识的了解程度,学校采用随机抽样的调查方式,根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.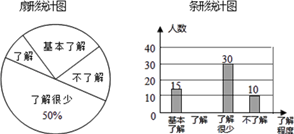
请你根据统计图中所提供的信息解答下列问题:
(1)、接受问卷调查的学生共有人.(2)、请补全条形统计图;(3)、若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.21. 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN. (1)、求证:四边形BMDN是菱形;(2)、若AB=4,AD=8,求MD的长.22. 某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)、求证:四边形BMDN是菱形;(2)、若AB=4,AD=8,求MD的长.22. 某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)、求A,B两种型号的机器人每小时分别搬运多少材料;
(2)、该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
23. 如图,已知AB是⊙O上的点,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.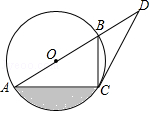 (1)、求证:CD是⊙O的切线;(2)、若∠D=30°,BD=2,求图中阴影部分的面积.24. 如图,Rt△AOB的顶点O在坐标原点,点B在x轴上,∠ABO=90°,反比例函数y= (x>0)的图象经过OA的中点C,交AB于点D,点C的坐标为( ,1),
(1)、求证:CD是⊙O的切线;(2)、若∠D=30°,BD=2,求图中阴影部分的面积.24. 如图,Rt△AOB的顶点O在坐标原点,点B在x轴上,∠ABO=90°,反比例函数y= (x>0)的图象经过OA的中点C,交AB于点D,点C的坐标为( ,1),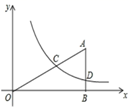 (1)、求反比例函数的表达式;(2)、连接CD,求四边形OCDB的面积.25. 某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)、求反比例函数的表达式;(2)、连接CD,求四边形OCDB的面积.25. 某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.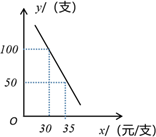 (1)、求y与x之间的函数关系式.(2)、由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?26. 在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.
(1)、求y与x之间的函数关系式.(2)、由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?26. 在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.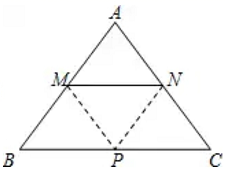 (1)、当MN为何值时,点P恰好落在BC上?(2)、当MN=x,△MNP与等腰△ABC重叠部分的面积为y,试写出y与x的函数关系式.当x为何值时,y的值最大,最大值是多少?
(1)、当MN为何值时,点P恰好落在BC上?(2)、当MN=x,△MNP与等腰△ABC重叠部分的面积为y,试写出y与x的函数关系式.当x为何值时,y的值最大,最大值是多少?