辽宁省沈阳市沈河区2020年数学中考一模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. ﹣2020的倒数是( )A、2020 B、± C、﹣ D、2. 2020年初全球处于新型冠状病毒引起的巨变之中,中国有2万名以上的医护人员在短时间就集结完毕,他们是我们心中的“最美逆行者”!其中数据2万用科学记数法表示为( )A、 2×103 B、2×104 C、0.2×105 D、20×1033. 如图,一个几何体由5个大小相同的正方体搭成,则这个立体图形的俯视图是( )
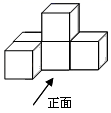 A、
A、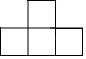 B、
B、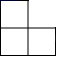 C、
C、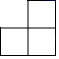 D、
D、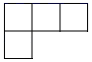 4. “2019武汉军运会”部分体育项目的示意图中是轴对称图形的是( )A、
4. “2019武汉军运会”部分体育项目的示意图中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 不等式组 的解集为( )A、
5. 不等式组 的解集为( )A、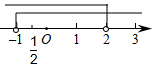 B、
B、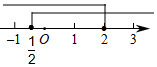 C、
C、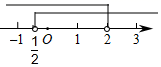 D、
D、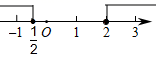 6. 如图,将一张矩形纸片折叠,若∠1=78°,则∠2的度数是( )
6. 如图,将一张矩形纸片折叠,若∠1=78°,则∠2的度数是( )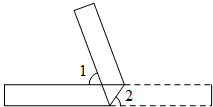 A、51° B、56° C、61° D、78°7.
A、51° B、56° C、61° D、78°7.《九章算术》是我国东汉初年编订的一部数学经典著作。在它的“方程”一章里,一次方程组是由算筹布置而成的,《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2,图中各行从左到右列出的算筹数分别表示未知数x , y的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是: ,类似地,图2所示的算筹图我们可以表述为( )
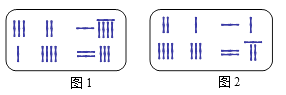 A、 B、 C、 D、8. 为了解某班学生每天使用零花钱的情况,小明随机调查了15名同学,结果如表:
A、 B、 C、 D、8. 为了解某班学生每天使用零花钱的情况,小明随机调查了15名同学,结果如表:每天使用零花钱(单位:元)
0
2
3
4
5
人数
1
4
5
3
2
关于这15名同学每天使用零花钱的情况,下列说法正确的是( )
A、中位数是3元 B、众数是5元 C、平均数是2.5元 D、方差是49. 如图,两条宽度都为1的纸条,交叉重叠放在一起,它们的夹角为锐角 ,它们重叠部分(阴影部分)的面积是1.5,那么 的值为( )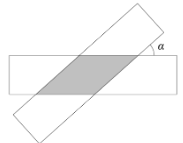 A、 B、 C、 D、10. 使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0°<x≤90°)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度可能为( )
A、 B、 C、 D、10. 使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)(0°<x≤90°)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度可能为( )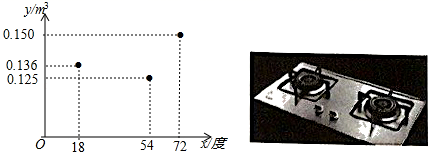 A、18° B、37° C、54° D、58°
A、18° B、37° C、54° D、58°二、填空题
-
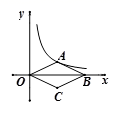
11. 分解因式:9ax2﹣ay2= .12. 若某正六边形的边长是 则该正六边形的边心距为.13. 关于x的一元二次方程x2﹣2x+k﹣1=0没有实数根,则k的取值范围是.14. 如图,在平面直角坐标系中,点O为原点,菱形OABC的对角线OB在x轴上,顶点A在反比例函数 的图象上,则菱形的面积为 .
 15. 某服装商预测一种应季衬衫能畅销市场,就用4000元购进一批衬衫,面市后果然供不应求,该服装商又用9000元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了5元.则该服装商第一批进货的单价是元.16. 如图,在网格纸中,每个小正方形的边长都是1个单位长度,每个小正方形的顶点叫做格点,点A,B,C,D均落在格点上,点E是AB的中点,过点E作EF∥AD,交BC于点F,作AG⊥EF,交FE延长线于点G,则线段EG的长度是.
15. 某服装商预测一种应季衬衫能畅销市场,就用4000元购进一批衬衫,面市后果然供不应求,该服装商又用9000元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了5元.则该服装商第一批进货的单价是元.16. 如图,在网格纸中,每个小正方形的边长都是1个单位长度,每个小正方形的顶点叫做格点,点A,B,C,D均落在格点上,点E是AB的中点,过点E作EF∥AD,交BC于点F,作AG⊥EF,交FE延长线于点G,则线段EG的长度是.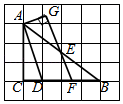
三、解答题
-
17. 计算: +| ﹣2|﹣2×cos30°+( )﹣1.18. 某商场开业,为了活跃气氛,用红、黄、蓝三色均分的转盘设计了两种抽奖方案,凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖(若指针恰好停在分割线上则重转).
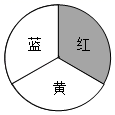
方案一:转动转盘一次,指针落在红色区域可领取一份奖品;
方案二:转动转盘两次,指针落在不同颜色区域可领取一份奖品.
(1)、若选择方案一,则可领取一份奖品的概率是;(2)、选择哪个方案可以使领取一份奖品的可能性更大?请用列表法或画树状图法说明理由.19. 我校为了了解九年级学生身体素质测试情况,随机抽取了本校九年级部分学生的身体素质测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如图不完整的统计图,请你结合图表所给信息解答下列问题: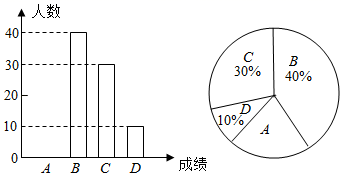 (1)、请在答题卡上直接将条形统计图补充完整;(2)、扇形统计图中“B”部分所对应的圆心角的度数是°;(3)、若我校九年级共有1500名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.20. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于点E,CF∥AE交AD延长线于点F.
(1)、请在答题卡上直接将条形统计图补充完整;(2)、扇形统计图中“B”部分所对应的圆心角的度数是°;(3)、若我校九年级共有1500名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.20. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于点E,CF∥AE交AD延长线于点F.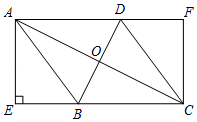 (1)、求证:四边形AECF是矩形;(2)、连接OE,若AE=12,AD=13,则线段OE的长度是.21. 如图,国庆节期间,小明一家自驾到某景区C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶6千米至B地,再沿北偏东45°方向行驶一段距离到达景区C,小明发现景区C恰好在A地的正北方向,求A,C两地相距多少千米?(结果保留根号)
(1)、求证:四边形AECF是矩形;(2)、连接OE,若AE=12,AD=13,则线段OE的长度是.21. 如图,国庆节期间,小明一家自驾到某景区C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶6千米至B地,再沿北偏东45°方向行驶一段距离到达景区C,小明发现景区C恰好在A地的正北方向,求A,C两地相距多少千米?(结果保留根号)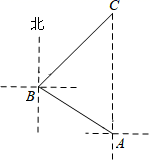 22. 如图,四边形ABCD内接于⊙O,点O在AB上,BC=CD,过点C作⊙O的切线,分别交AB,AD的延长线于点E,F.
22. 如图,四边形ABCD内接于⊙O,点O在AB上,BC=CD,过点C作⊙O的切线,分别交AB,AD的延长线于点E,F.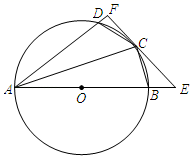 (1)、求证:AF⊥EF;(2)、若cos∠DAB= ,BE=1,则线段AD的长是.23. 如图,在平面直角坐标系中,矩形OABC边OA,OC分别在x轴,y的正半轴上,且OA=8,OC=6,连接AC,点D为AC中点,点E从点C出发以每秒1个单位长度运动到点O停止,设运动时间为t秒(0<t<6),连接DE,作DF⊥DE交OA于点F,连接EF.
(1)、求证:AF⊥EF;(2)、若cos∠DAB= ,BE=1,则线段AD的长是.23. 如图,在平面直角坐标系中,矩形OABC边OA,OC分别在x轴,y的正半轴上,且OA=8,OC=6,连接AC,点D为AC中点,点E从点C出发以每秒1个单位长度运动到点O停止,设运动时间为t秒(0<t<6),连接DE,作DF⊥DE交OA于点F,连接EF.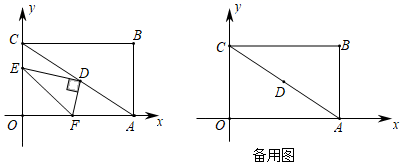 (1)、当t的值为时,四边形DEOF是矩形;(2)、用含t的代数式表示线段OF的长度,并说明理由;(3)、当△OEF面积为 时,请直接写出直线DE的解析式.24. 思维探索:
(1)、当t的值为时,四边形DEOF是矩形;(2)、用含t的代数式表示线段OF的长度,并说明理由;(3)、当△OEF面积为 时,请直接写出直线DE的解析式.24. 思维探索:在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
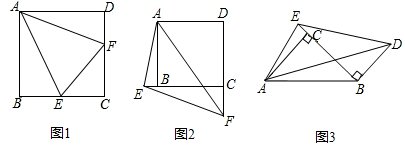 (1)、如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是;(2)、如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;25. 在平面直角坐标系中,抛物线y=ax2+bx+ 与x轴分别交于点A(﹣1,0),B(3,0),点C是顶点.
(1)、如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是;(2)、如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;25. 在平面直角坐标系中,抛物线y=ax2+bx+ 与x轴分别交于点A(﹣1,0),B(3,0),点C是顶点.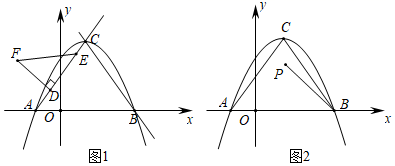 (1)、求抛物线的解析式;(2)、如图1,线段DE是射线AC上的一条动线段(点D在点E的下方),且DE=2,点D从点A出发沿着射线AC的方向以每秒2个单位长度的速度运动,以DE为一边在AC上方作等腰Rt△DEF,其中∠EDF=90°,设运动时间为t秒.
(1)、求抛物线的解析式;(2)、如图1,线段DE是射线AC上的一条动线段(点D在点E的下方),且DE=2,点D从点A出发沿着射线AC的方向以每秒2个单位长度的速度运动,以DE为一边在AC上方作等腰Rt△DEF,其中∠EDF=90°,设运动时间为t秒.①点D的坐标是 ▲ (用含t的代数式表示);
②当直线BC与△DEF有交点时,请求出t的取值范围;
(3)、如图2,点P是△ABC内一动点,BP= ,点M,N分别是AB,BC边上的两个动点,当△PMN的周长最小时,请直接写出四边形PNBM面积的最大值.