辽宁省抚顺市新抚区2020年数学中考三模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. 的倒数是 ( )A、2 B、-2 C、 D、2. 下列运算正确的是( )A、﹣2(a﹣1)=﹣2a﹣1 B、(﹣2a)2=﹣2a2 C、3x2﹣2x2=x2 D、(2a+b)2=4a2+b23. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 辽宁号航空母舰是中国人民解放军海军第一艘服役的航空母舰.满载时排水量为67500吨,将数据67500用科学记数法表示为( )A、6.75×103 B、6.75×104 C、0.675×105 D、675×1025. 在“经典诵读”比赛活动中,某校10名学生参赛成绩如图所示,对于这10名学生的参赛成绩,下列说法正确的是( )
4. 辽宁号航空母舰是中国人民解放军海军第一艘服役的航空母舰.满载时排水量为67500吨,将数据67500用科学记数法表示为( )A、6.75×103 B、6.75×104 C、0.675×105 D、675×1025. 在“经典诵读”比赛活动中,某校10名学生参赛成绩如图所示,对于这10名学生的参赛成绩,下列说法正确的是( )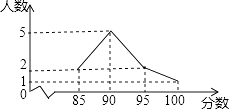 A、众数是90分 B、中位数是95分 C、平均数是95分 D、方差是156. 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是( )
A、众数是90分 B、中位数是95分 C、平均数是95分 D、方差是156. 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是( )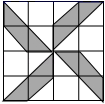 A、 B、 C、 D、7. 为了践行“绿水青山就是金山银山”的理念.地计划将420亩荒山进行绿化,实际绿化时,工作效率是原计划的1.5倍,进而比原计划提前2天完成绿化任务,设原来平均每天绿化荒山x亩,可列方程为( )A、 B、 C、 D、8. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
A、 B、 C、 D、7. 为了践行“绿水青山就是金山银山”的理念.地计划将420亩荒山进行绿化,实际绿化时,工作效率是原计划的1.5倍,进而比原计划提前2天完成绿化任务,设原来平均每天绿化荒山x亩,可列方程为( )A、 B、 C、 D、8. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )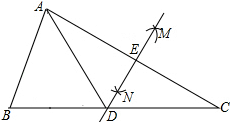 A、16cm B、19cm C、22cm D、25cm9. 如图所示,点B、D在双曲线 上,点A在双曲线 上,且 轴, 轴, 以AB、AD为邻边作平行四边形ABCD,则平行四边形ABCD的面积是( )
A、16cm B、19cm C、22cm D、25cm9. 如图所示,点B、D在双曲线 上,点A在双曲线 上,且 轴, 轴, 以AB、AD为邻边作平行四边形ABCD,则平行四边形ABCD的面积是( ) A、6 B、8 C、10 D、1210. 正方形ABCD的边长为4,P 为BC上的动点,连接PA,作PQ⊥PA,PQ交CD于Q,连接AQ ,则AQ的最小值是( )
A、6 B、8 C、10 D、1210. 正方形ABCD的边长为4,P 为BC上的动点,连接PA,作PQ⊥PA,PQ交CD于Q,连接AQ ,则AQ的最小值是( )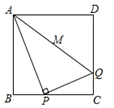 A、5 B、 C、 D、4
A、5 B、 C、 D、4二、填空题
-
11. 计算: .12. 关于x的一元二次方程x2-4x+m=0有两个不相等的实数根,则实数m的取值范是.13. 从1,2,3,4,5这5个数中任取2个数,组成两位数,则这个两位数能被3整除的概率是14. 已知抛物线y=ax2+bx+c(a>0)的顶点为(2,4),若点(﹣2,m),(3,n)在抛物线上,则mn(填“>”、“=”或“<”).15. 如图,直线a∥b,∠1=120°,∠2=105°,则∠3的度数为
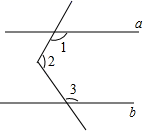 16. 一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺ABC绕着点C按逆时针方向旋转n°后(0<n<360 ),若ED⊥AB,则n的值是.
16. 一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺ABC绕着点C按逆时针方向旋转n°后(0<n<360 ),若ED⊥AB,则n的值是.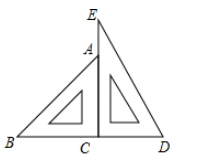 17. 如图,点A是反比例函数y= 的图象上一点,点B在y轴的正半轴上,连接OA,AB且∠OAB=90°,OA=4,AB=2,则k=
17. 如图,点A是反比例函数y= 的图象上一点,点B在y轴的正半轴上,连接OA,AB且∠OAB=90°,OA=4,AB=2,则k= 18. 如图,点A1(2,1)在直线y=kx上,过点A1作A1B1∥y轴交x轴于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=kx和x轴于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则带点Cn的坐标为.(结果用含正整数n的代数式表示)
18. 如图,点A1(2,1)在直线y=kx上,过点A1作A1B1∥y轴交x轴于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=kx和x轴于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则带点Cn的坐标为.(结果用含正整数n的代数式表示)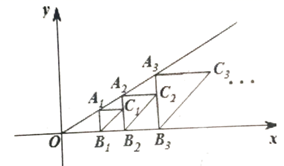
三、解答题
-
19. 先化简再求值: 选一个使原代数式有意义的数代入求值.20. (抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。
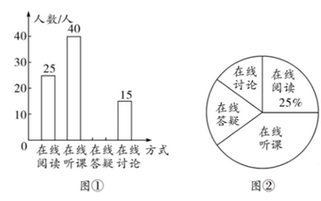 (1)、本次调查的人数有多少人?(2)、请补全条形图;(3)、请求出“在线答疑”在扇形图中的圆心角度数;(4)、小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.21. 有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?(2)、某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.22. 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)、本次调查的人数有多少人?(2)、请补全条形图;(3)、请求出“在线答疑”在扇形图中的圆心角度数;(4)、小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.21. 有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?(2)、某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.22. 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.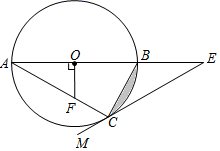 (1)、求证:EM是⊙O的切线;(2)、若∠A=∠E,⊙O的半径为1,求阴影部分的面积.23. 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.选凉亭A,C作为观测点.如图,现测得∠CAB=45°,∠ACB=98°,AC=200米,请计算A,B两个凉亭之间的距离、(结果精确到1米)(参考数据: ≈1.414, ≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
(1)、求证:EM是⊙O的切线;(2)、若∠A=∠E,⊙O的半径为1,求阴影部分的面积.23. 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.选凉亭A,C作为观测点.如图,现测得∠CAB=45°,∠ACB=98°,AC=200米,请计算A,B两个凉亭之间的距离、(结果精确到1米)(参考数据: ≈1.414, ≈1.732,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)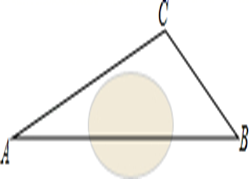 24. 我市某乡镇实施产业精准扶贫,帮助贫困户承包了若干亩土地种植新品草莓,已知该草莓的成本为每千克10元,草莓成熟后投入市场销售,经市场调查发现,草莓销售不会亏本,且每天的销售量y(千克)与销售单价x(元/千克)之间函数关系如图所示.
24. 我市某乡镇实施产业精准扶贫,帮助贫困户承包了若干亩土地种植新品草莓,已知该草莓的成本为每千克10元,草莓成熟后投入市场销售,经市场调查发现,草莓销售不会亏本,且每天的销售量y(千克)与销售单价x(元/千克)之间函数关系如图所示.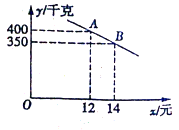 (1)、求y与x的函数关系式,并写出x的取值范围.(2)、当该品种草莓的定价为多少时,每天销售获得利润最大?最大利润是多少?(3)、某村今年草莓采摘期限30天,预计产量6000千克,则按照(2)中的方式进行销售,能否销售完这批草莓?请说明理由.25. 如图,四边形ABCD为正方形,E为对角线BD上的动点,过点E作FG⊥AE,FG交射线CD于F,交射线CB于G.
(1)、求y与x的函数关系式,并写出x的取值范围.(2)、当该品种草莓的定价为多少时,每天销售获得利润最大?最大利润是多少?(3)、某村今年草莓采摘期限30天,预计产量6000千克,则按照(2)中的方式进行销售,能否销售完这批草莓?请说明理由.25. 如图,四边形ABCD为正方形,E为对角线BD上的动点,过点E作FG⊥AE,FG交射线CD于F,交射线CB于G.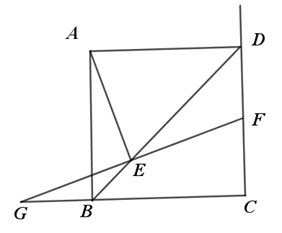 (1)、求证:EF=EG(2)、求证:(3)、若AB=4,当∠GEB=22.5°,直接写出CF的长.26. 如图,直线y= x+4与x轴交于点A,与y轴交于点B,抛物线y=﹣ x2+bx+c经过A,B两点,与x轴正半轴交于点C,连接BC,P为线段AC上的动点,P与A,C不重合,作PQ∥BC交AB于点Q,A关于PQ的对称点为D,连接PD,QD,BD.
(1)、求证:EF=EG(2)、求证:(3)、若AB=4,当∠GEB=22.5°,直接写出CF的长.26. 如图,直线y= x+4与x轴交于点A,与y轴交于点B,抛物线y=﹣ x2+bx+c经过A,B两点,与x轴正半轴交于点C,连接BC,P为线段AC上的动点,P与A,C不重合,作PQ∥BC交AB于点Q,A关于PQ的对称点为D,连接PD,QD,BD.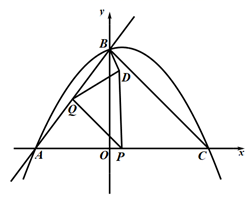 (1)、求抛物线的解析式;(2)、当点D在抛物线上时,求点P的坐标.(3)、设点P的横坐标为x,△PDQ与△ABC的重叠部分的面积为S
(1)、求抛物线的解析式;(2)、当点D在抛物线上时,求点P的坐标.(3)、设点P的横坐标为x,△PDQ与△ABC的重叠部分的面积为S①直接写出S与x的函数关系式;
②当△BDQ为直角三角形时,直接写出x的值.