辽宁省大连市中山区2020年数学中考一模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. 实数4的相反数是( )
A、 B、-4 C、 D、42. 如图是由4个相同的小正方体组成的一个立体图形,其主视图是( )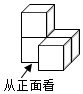 A、
A、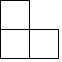 B、
B、 C、
C、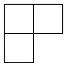 D、
D、 3. 年 月 日 时 分,“嫦娥四号”探测器飞行约 千米,实现人类探测器首次在月球背面软着陆.数据 用科学记数法表示为( )A、 B、 C、 D、4. 在平面直角坐标系xOy中,将点N(–1,–2)绕点O旋转180°,得到的对应点的坐标是( )A、(1,2) B、(–1,2) C、(–1,–2) D、(1,–2)5. 不等式组 的解集是( )A、 B、 或 C、 D、6. 下列图形,既是轴对称图形又是中心对称图形的是( )A、正三角形 B、正五边形 C、等腰直角三角形 D、矩形7. 化简(2x)2的结果是( )A、x4 B、2x2 C、4x2 D、4x8. 在同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为( )A、 B、 C、 D、9. 如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为( )
3. 年 月 日 时 分,“嫦娥四号”探测器飞行约 千米,实现人类探测器首次在月球背面软着陆.数据 用科学记数法表示为( )A、 B、 C、 D、4. 在平面直角坐标系xOy中,将点N(–1,–2)绕点O旋转180°,得到的对应点的坐标是( )A、(1,2) B、(–1,2) C、(–1,–2) D、(1,–2)5. 不等式组 的解集是( )A、 B、 或 C、 D、6. 下列图形,既是轴对称图形又是中心对称图形的是( )A、正三角形 B、正五边形 C、等腰直角三角形 D、矩形7. 化简(2x)2的结果是( )A、x4 B、2x2 C、4x2 D、4x8. 在同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为( )A、 B、 C、 D、9. 如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为( ) A、 B、4 C、4.5 D、510. 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
A、 B、4 C、4.5 D、510. 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( ) A、ac+1=b B、ab+1=c C、bc+1=a D、以上都不是
A、ac+1=b B、ab+1=c C、bc+1=a D、以上都不是二、填空题
-
11. 如图,E为△ABC边CA延长线上一点,过点E作ED∥BC.若∠BAC=70°,∠CED=50°,则∠B=°.
 12. 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=.
12. 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=.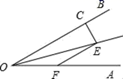 13. 为了建设“书香校园”,某校七年级的同学积极捐书,下表统计了七(1)班40名学生的捐书情况:
13. 为了建设“书香校园”,某校七年级的同学积极捐书,下表统计了七(1)班40名学生的捐书情况:捐书(本)
3
4
5
7
10
人数
5
7
10
11
7
该班学生平均每人捐书本.
14. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 两,牛每头 两,根据题意可列方程组为.15. 如图,无人机于空中 处测得某建筑顶部 处的仰角为 ,测得该建筑底部 处的俯角为 .若无人机的飞行高度 为 ,则该建筑的高度 为 .(参考数据: , , ) 16. 甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是米.
16. 甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是米.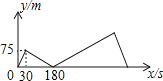
三、解答题
-
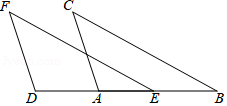
17. 计算:18. 化简:19. 如图,EF=BC,DF=AC,DA=EB.求证:∠F=∠C.
 20. 某校为了解九年级学生每天参加体育锻炼额时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):
20. 某校为了解九年级学生每天参加体育锻炼额时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):30 60 70 10 30 115 70 60 75 90 15 70 40 75 105 80 60 30 70 45
对以上数据进行整理分析,得到下列表一和表二:
表一
时间t(单位:分钟)
人数
2
a
10
b
表二
平均数
中位数
众数
60
c
d
根据以上提供信息,解答下列问题:
(1)、填空①a= b=
②c= d=
(2)、如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数。21. 改善小区环境,争创文明家园.如图所示,某社区决定在一块长( )16 ,宽( )9 的矩形场地 上修建三条同样宽的小路,其中两条与 平行,另一条与 平行,其余部分种草.要使草坪部分的总面积为112 ,则小路的宽应为多少? 22. 如图,函数 的图象与函数 (x>0)的图象相交于点P(4,m).
22. 如图,函数 的图象与函数 (x>0)的图象相交于点P(4,m).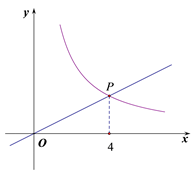 (1)、求m,k的值;(2)、直线y=3与函数 的图象相交于点A,与函数 (x>0)的图象相交于点B,求线段AB长.23. 如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且DE是⊙O的切线.
(1)、求m,k的值;(2)、直线y=3与函数 的图象相交于点A,与函数 (x>0)的图象相交于点B,求线段AB长.23. 如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且DE是⊙O的切线.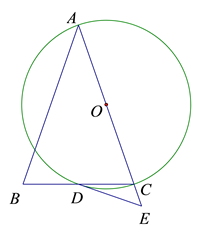 (1)、求证:∠CDE= ∠BAC;(2)、若AB=3BD,CE=4,求⊙O的半径.24. 如图,在平面直角坐标系xOy中,直线 与y轴,x轴分别相交于点A、B.点D是x轴上动点,点D从点B出发向原点O运动,点E在点D右侧,DE=2BD.过点D作DH⊥AB于点H,将△DBH沿直线DH翻折,得到△DCH,连接CE.设BD=t,△DCE与△AOB重合部分面积为S.求:
(1)、求证:∠CDE= ∠BAC;(2)、若AB=3BD,CE=4,求⊙O的半径.24. 如图,在平面直角坐标系xOy中,直线 与y轴,x轴分别相交于点A、B.点D是x轴上动点,点D从点B出发向原点O运动,点E在点D右侧,DE=2BD.过点D作DH⊥AB于点H,将△DBH沿直线DH翻折,得到△DCH,连接CE.设BD=t,△DCE与△AOB重合部分面积为S.求: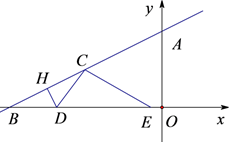 (1)、求线段BC的长(用含t的代数式表示);(2)、求S关于t的函数解析式,并直接写出自变量t的取值范围.25. 阅读下面材料,完成(1)-(3)题.
(1)、求线段BC的长(用含t的代数式表示);(2)、求S关于t的函数解析式,并直接写出自变量t的取值范围.25. 阅读下面材料,完成(1)-(3)题.数学课上,老师出示了这样一道题:
如图1,在△ABC中,BA=BC, .点F在AC上,点E在BF上, .点D在BC 延长线上,连接AD、AE,∠ACD+∠DAE=180゜.探究线段AD与AE的数量关系并证明.
同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现∠CAD与∠EAB相等.”
小亮:“通过观察和度量,发现∠FAE与∠D也相等.”
小伟:“通过边角关系构造辅助线,经过进一步推理,可以得到线段AD与AE的数量关系.”
老师:“保留原题条件,延长图1中的AE,与BC相交于点H(如图2),若知道DH与
AH的数量关系,可以求出 的值.”
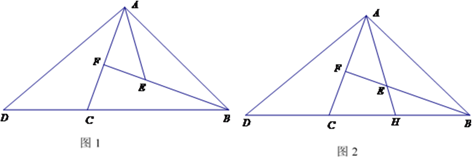 (1)、求证:∠CAD=∠EAB;(2)、求 的值(用含k的式子表示);(3)、如图2,若 ,则 的值为(用含k的式子表示).26. 已知抛物线 过点A(m-2,n), B(m+4,n),C(m, ).(1)、b=(用含m的代数式表示);(2)、求△ABC的面积;(3)、当 时,均有 ,求m的值.
(1)、求证:∠CAD=∠EAB;(2)、求 的值(用含k的式子表示);(3)、如图2,若 ,则 的值为(用含k的式子表示).26. 已知抛物线 过点A(m-2,n), B(m+4,n),C(m, ).(1)、b=(用含m的代数式表示);(2)、求△ABC的面积;(3)、当 时,均有 ,求m的值.