江苏省扬州市江都区2020年数学中考二模试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. 下列所给图形是中心对称图形但不是轴对称图形的是( )A、
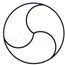 B、
B、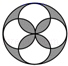 C、
C、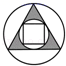 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 下列根式中,不能与合并的是( )A、 B、 C、 D、4. 下列长度的三条线段能组成直角三角形的是( )A、5,11,12 B、5,12,13 C、4,5,6 D、 ,2,5. 图是由6个相同的小立方块搭成的几何体,那么这个几何体的俯视图是( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 下列根式中,不能与合并的是( )A、 B、 C、 D、4. 下列长度的三条线段能组成直角三角形的是( )A、5,11,12 B、5,12,13 C、4,5,6 D、 ,2,5. 图是由6个相同的小立方块搭成的几何体,那么这个几何体的俯视图是( )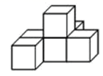 A、
A、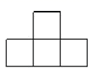 B、
B、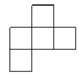 C、
C、 D、
D、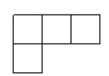 6. 如图,平行于x轴的直线与函数 , 的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若 的面积为4,则 的值为 )
6. 如图,平行于x轴的直线与函数 , 的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若 的面积为4,则 的值为 )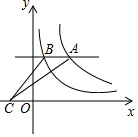 A、8 B、-8 C、4 D、-47. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
A、8 B、-8 C、4 D、-47. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( ) A、abc<0 B、b2﹣4ac<0 C、a﹣b+c<0 D、2a+b=08. 如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线 对折,点O恰好落在∠OAB的平分线上的O’处,则b的值为( )
A、abc<0 B、b2﹣4ac<0 C、a﹣b+c<0 D、2a+b=08. 如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线 对折,点O恰好落在∠OAB的平分线上的O’处,则b的值为( )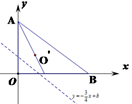 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. -5的倒数是 , 精确到.10. 分解因式: .11. 肆虐全球的新型冠状病毒直径大约为125纳米,即0.000000125米.请你将0.000000125用科学记数法表示为米.12. 在平面直角坐标系中,点 关于原点 的对称点的坐标是.13. 若一个多边形的内角和比外角和大360°,则这个多边形的边数为 .14. 若双曲线 与直线 无交点,则k的取值范围是.15. 如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE.若BC=12,S△BCE=24,则tanC=.
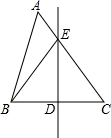 16. 已知点P(1-a,2a+6)在第四象限,则a的取值范围是.17. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r =4,扇形的圆心角θ=120°,则该圆锥母线l的长为.
16. 已知点P(1-a,2a+6)在第四象限,则a的取值范围是.17. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r =4,扇形的圆心角θ=120°,则该圆锥母线l的长为.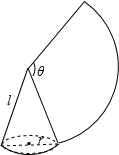 18. 如图,在正方形ABCD中,AB=4,以B为圆心,BA长为半径画弧,点M为弧上一点,MN⊥CD于N,连接CM,则CM-MN的最大值为 .
18. 如图,在正方形ABCD中,AB=4,以B为圆心,BA长为半径画弧,点M为弧上一点,MN⊥CD于N,连接CM,则CM-MN的最大值为 .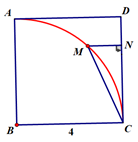
三、解答题
-
19.(1)、计算:(2)、解方程:20. 化简: ÷(x﹣ ),再从1、0、 中选一个数代入求值.21. 从1名男生和3名女生中随机抽取参加“我爱苏州”演讲比赛的同学.(1)、若抽取1名,恰好是男生的概率为;(2)、若抽取2名,求恰好是2名女生的概率.(用树状图或列表法求解)22. 某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况:
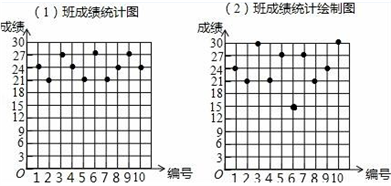 (1)、利用图中提供的信息,补全下表:
(1)、利用图中提供的信息,补全下表: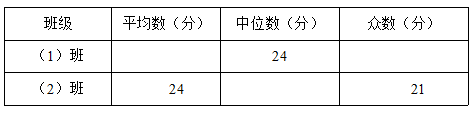 (2)、若把24分以上(含24分)记为”优秀”,两班各50名学生,请估计两班各有多少名学生成绩优秀;(3)、观察图中数据分布情况,请通过计算方差说明哪个班的学生纠错的得分情况更稳定.23. “母亲节”前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着又用5000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价是多少元?24. 如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
(2)、若把24分以上(含24分)记为”优秀”,两班各50名学生,请估计两班各有多少名学生成绩优秀;(3)、观察图中数据分布情况,请通过计算方差说明哪个班的学生纠错的得分情况更稳定.23. “母亲节”前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着又用5000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价是多少元?24. 如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.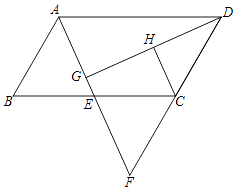 (1)、求证:△ABE≌△FCE;(2)、过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系,
(1)、求证:△ABE≌△FCE;(2)、过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系,并说明理由.
 25. 如图,四边形ABCD是⊙O的内接四边形,AC为直径, ,DE⊥BC,垂足为E.
25. 如图,四边形ABCD是⊙O的内接四边形,AC为直径, ,DE⊥BC,垂足为E. (1)、求证:CD平分∠ACE;(2)、判断直线ED与⊙O的位置关系,并说明理由;(3)、若CE=2,AC=8,阴影部分的面积为.26. 在平面直角坐标系中,过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则称这个点为强点.例如,图中过点P分別作x轴,y轴的垂线与坐标轴围成矩形OAPB的周长与面积相等,则点P是强点.
(1)、求证:CD平分∠ACE;(2)、判断直线ED与⊙O的位置关系,并说明理由;(3)、若CE=2,AC=8,阴影部分的面积为.26. 在平面直角坐标系中,过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则称这个点为强点.例如,图中过点P分別作x轴,y轴的垂线与坐标轴围成矩形OAPB的周长与面积相等,则点P是强点.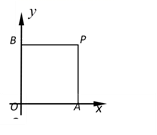 (1)、点M(l,2),N(4,4),Q(6,-3)中,是强点的有;(2)、若强点P(2a,3)在双曲线 上,求a和b的值.27. 绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.
(1)、点M(l,2),N(4,4),Q(6,-3)中,是强点的有;(2)、若强点P(2a,3)在双曲线 上,求a和b的值.27. 绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.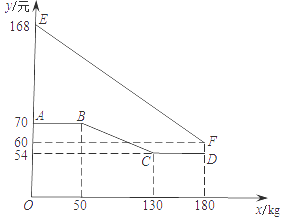 (1)、求该产品销售价y1(元)与产量x(kg)之间的函数关系式;(2)、直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;(3)、当产量为多少时,这种产品获得的利润最大?最大利润为多少?28. 如图,抛物线y=ax2+bx+c(a、b、c是常数,a≠0)经过原点O和 两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0, 2).
(1)、求该产品销售价y1(元)与产量x(kg)之间的函数关系式;(2)、直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;(3)、当产量为多少时,这种产品获得的利润最大?最大利润为多少?28. 如图,抛物线y=ax2+bx+c(a、b、c是常数,a≠0)经过原点O和 两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0, 2).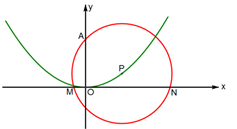 (1)、a= , b= , c=;(2)、求证:在点P运动的过程中,⊙P始终与x轴相交;(3)、设⊙P与x轴相交于M、N两点,M在N的左边.当△AMN为等腰三角形时,直接写出圆心P的横坐标.
(1)、a= , b= , c=;(2)、求证:在点P运动的过程中,⊙P始终与x轴相交;(3)、设⊙P与x轴相交于M、N两点,M在N的左边.当△AMN为等腰三角形时,直接写出圆心P的横坐标.