江苏省扬州市广陵区2020年数学中考模拟试卷
试卷更新日期:2020-07-22 类型:中考模拟
一、选择题
-
1. -2的倒数是( )A、- B、 C、±2 D、22. 函数y= 中自变量x的取值范围是( )A、x>2 B、x≤2 C、x≥2 D、x≠23. 下列计算正确的是( )A、2a+3b=5ab B、(a-b)2=a2-b2 C、(2x2)3=6x6 D、x8÷x3=x54. 下列水平放置的四个几何体中,主视图与其它三个不相同的是( )A、
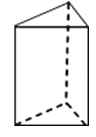 B、
B、 C、
C、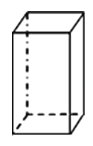 D、
D、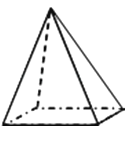 5. 已知正多边形的一个内角是140°,则这个正多边形的边数是( )A、九边形 B、八边形 C、七边形 D、六边形6. 丽华根据演讲比赛中九位评委所给的分数作了如下表格
5. 已知正多边形的一个内角是140°,则这个正多边形的边数是( )A、九边形 B、八边形 C、七边形 D、六边形6. 丽华根据演讲比赛中九位评委所给的分数作了如下表格平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A、平均数 B、众数 C、方差 D、中位数7. 在二次函数 中,函数y与自变量x的部分对应值如下表:x
1
2
3
4
5
6
y
2
m
n
则m、n的大小关系为
A、 B、 C、 D、无法比较8. 两块等腰直角三角形纸片AOB和COD 按图1所示放置,直角顶点重合在点O处,其中AB=3 ,CD=6.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°),如图2所示.当BD与CD在同一直线上(如图3)时,tanα的值等于( )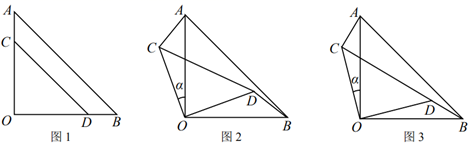 A、 B、 C、 D、9. 我国最大的领海南海总面积有3500 000平方公里,将数3500 000用科学记数法表示应为 .10. 若2x=3y,且x≠0,则 的值为.11. 若关于x的方程x2﹣8x+m=0有两个相等的实数根,则m= .12. 如图,转盘中6个小扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向红色区域的概率为.
A、 B、 C、 D、9. 我国最大的领海南海总面积有3500 000平方公里,将数3500 000用科学记数法表示应为 .10. 若2x=3y,且x≠0,则 的值为.11. 若关于x的方程x2﹣8x+m=0有两个相等的实数根,则m= .12. 如图,转盘中6个小扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向红色区域的概率为. 13. 如图,将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上,如果∠1=27°,那么∠2=°
13. 如图,将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上,如果∠1=27°,那么∠2=°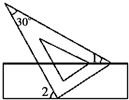 14. 圆锥的底面半径为2,母线长为4,则圆锥的侧面积为(结果保留π)15. 如图,⊙O的内接四边形ABCD中,∠BOD=100°,则∠BCD=.
14. 圆锥的底面半径为2,母线长为4,则圆锥的侧面积为(结果保留π)15. 如图,⊙O的内接四边形ABCD中,∠BOD=100°,则∠BCD=. 16. 计算:40382-4×2018×2020=.17. 如图,菱形OABC中点A的坐标是(2,1),点B的横坐标是3,则点C的坐标是.
16. 计算:40382-4×2018×2020=.17. 如图,菱形OABC中点A的坐标是(2,1),点B的横坐标是3,则点C的坐标是.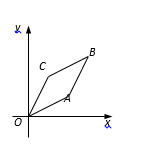 18. 如图,将直线y=x向下平移b个单位长度后得到直线 , 与反比例函数 (k>0,x>0)的图象相交于点A,与x轴相交于点B,且 ,则k的值是.
18. 如图,将直线y=x向下平移b个单位长度后得到直线 , 与反比例函数 (k>0,x>0)的图象相交于点A,与x轴相交于点B,且 ,则k的值是.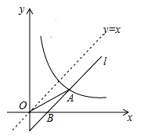
二、解答题
-
19.(1)、计算: ;(2)、解不等式: .20. 先化简再求值: ,其中 是方程 的一个根.21. 为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段
(小时/周)
小丽抽样
人数
小杰抽样
人数
0~1
6
22
1~2
10
10
2~3
16
6
3~4
8
2
(每组可含最低值,不含最高值)
 (1)、你认为哪位同学抽取的样本不合理?请说明理由;(2)、根据合理抽取的样本,把上图中的频数分布直方图补画完整;(3)、专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?22. 在不透明的袋子中有四张标着数字 , , , 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.下图是他所画的树状图的一部分.
(1)、你认为哪位同学抽取的样本不合理?请说明理由;(2)、根据合理抽取的样本,把上图中的频数分布直方图补画完整;(3)、专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?22. 在不透明的袋子中有四张标着数字 , , , 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.下图是他所画的树状图的一部分.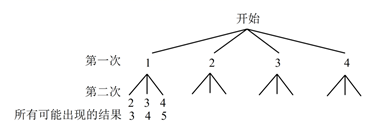 (1)、由上图分析,甲同学的游戏规则是:从袋子中随机抽出一张卡片后(填"放回"或"不放回"),再随机抽出一张卡片;(2)、帮甲同学完成树状图;(3)、求甲同学两次抽到的数字之和为偶数的概率.23. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、由上图分析,甲同学的游戏规则是:从袋子中随机抽出一张卡片后(填"放回"或"不放回"),再随机抽出一张卡片;(2)、帮甲同学完成树状图;(3)、求甲同学两次抽到的数字之和为偶数的概率.23. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.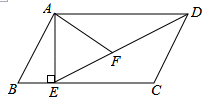 (1)、在图中找出一对相似三角形,并说明理由;(2)、若AB=8,AD= ,AF= ,求AE的长.24. 甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.
(1)、在图中找出一对相似三角形,并说明理由;(2)、若AB=8,AD= ,AF= ,求AE的长.24. 甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
25. 如图,AB是⊙O的直径, BC交⊙O于点D,E是 的中点,连接AE交BC于点F,∠ACB =2∠EAB.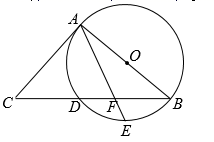 (1)、判断直线AC与⊙O的位置关系,并说明理由;(2)、若 , ,求BF的长.26. 如图①,老旧电视机屏幕的长宽比为4︰3,但是多数电影图象的长宽比为2.4︰1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
(1)、判断直线AC与⊙O的位置关系,并说明理由;(2)、若 , ,求BF的长.26. 如图①,老旧电视机屏幕的长宽比为4︰3,但是多数电影图象的长宽比为2.4︰1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.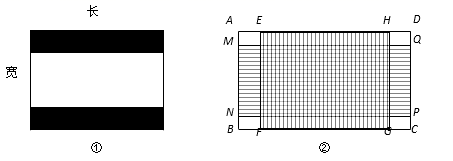 (1)、若图①中电视机屏幕为20寸(即屏幕对角线长度):
(1)、若图①中电视机屏幕为20寸(即屏幕对角线长度):①该屏幕的长= ▲ 寸,宽= ▲ 寸;
②已知“屏幕浪费比=黑色带子的总面积:电视机屏幕的总面积”,求该电视机屏幕的浪费比.
(2)、为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(矩形ABCD)恰好包含面积相等且长宽比分别为4︰3的屏幕(矩形EFGH)与2.4︰1的屏幕(矩形MNPQ).求这种屏幕的长宽比.(参考数据: ≈2.2,结果精确到0.1)27. 如图1,对角线互相垂直的四边形叫做垂美四边形. (1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)、性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;(3)、解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.28. 如图,抛物线 过点 ,且与直线 交于B、C两点,点B的坐标为 .
(1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)、性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;(3)、解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.28. 如图,抛物线 过点 ,且与直线 交于B、C两点,点B的坐标为 .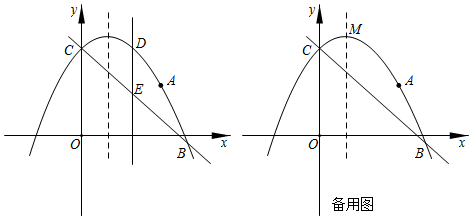 (1)、求抛物线的解析式;(2)、点D为抛物线上位于直线 上方的一点,过点D作 轴交直线 于点E , 点P为对称轴上一动点,当线段 的长度最大时,求 的最小值;(3)、设点M为抛物线的顶点,在y轴上是否存在点Q , 使 ?若存在,求点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点D为抛物线上位于直线 上方的一点,过点D作 轴交直线 于点E , 点P为对称轴上一动点,当线段 的长度最大时,求 的最小值;(3)、设点M为抛物线的顶点,在y轴上是否存在点Q , 使 ?若存在,求点Q的坐标;若不存在,请说明理由.