江苏省盐城市射阳县2020年数学中考一模试卷

试卷更新日期：2020-07-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 实数a、b、c、d在数轴上的对应点的位置如图所示，在这四个数中，绝对值最小的数是（）

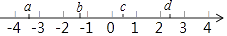A、a B、b C、c D、d

查看试题解析
2. 下列四张扑克牌的牌面，不是中心对称图形的（）

A、 B、 C、 D、

查看试题解析
3. 今年以来，人们对全国多地大范围持续的雾霾天气记忆犹新，“细颗粒物PM2.5”遂成为显示度最高的热词之一.PM2.5是指大气中直径小于或等于0.0000025米（2.5微米）的颗粒物，也称为可入肺颗粒物.把0.0000025用科学记数法表示为（）

A、 $0.25 \times 10^{- 5}$ B、 $2.5 \times 10^{- 5}$ C、 $2.5 \times 10^{- 6}$ D、 $25 \times 10^{- 7}$

查看试题解析
4. 如图所示的正三棱柱，它的主视图、俯视图、左视图的顺序是（）

A、①②③ B、②①③ C、③①② D、①③②

查看试题解析
5. 圆的直径是8cm，若圆心与直线的距离是4cm，则该直线和圆的位置关系是（）

A、相离 B、相切 C、相交 D、相交或相切

查看试题解析
6. 下列运算正确的是（）

A、 $3 x - 2 x = x$ B、 $3 x + 2 x = 5 x^{2}$ C、 $3 x \cdot 2 x = 6 x$ D、 $3 x \div 2 x = \frac{2}{3}$

查看试题解析
7. 若关于x的二次三项式x²+kx+b因式分解为（x﹣1）（x﹣3），则k+b的值为（）

A、﹣1 B、1 C、﹣7 D、7

查看试题解析
8. 如图1是一座立交桥的示意图（道路宽度忽略不计），A为入口，F，G为出口，其中直行道为AB，CG，EF，且AB＝CG＝EF；弯道为以点O为圆心的一段弧，且所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥，均以8m/s的速度行驶，从不同出口驶出，其间两车到点O的距离y（m）与时间x（s）的对应关系如图2所示，结合题目信息，下列说法错误的是（）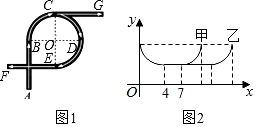

A、立交桥总长为168 m B、从F口出比从G口出多行驶48m C、甲车在立交桥上共行驶11 s D、甲车从F口出，乙车从G口出

查看试题解析

二、填空题

9. 要使二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
10. 9的平方根是，使分式 $\frac{1}{x + 1}$ 有意义的x的取值范围是．

查看试题解析
11. 在平面直角坐标系中，点A（2，1）关于x轴对称的点的坐标是.

查看试题解析
12. 分解因式：9x²－y²＝.

查看试题解析
13. 小华5次射击的成绩如下：（单位：环）5，9，7，10，9．其方差为3.2，如果他再射击1次，命中8环，那么他的射击成绩的方差．（填“变大”、“变小”或“不变”）

查看试题解析
14. 在半径为2 cm的⊙O中，用刻度尺（单位：cm）测得弦AB的长如图所示，则劣弧AB的长为cm.

查看试题解析
15. 如图， $△ A B C$ 中， $D ， E$ 两点分别在 $A B$ ， $B C$ 上，若 $B D ： B A = B E ： B C = 1 ： 3$ ，则 $△ D B E$ 的面积： $△ A D C$ 的面积 $=$ .

查看试题解析
16. 如图，点A在双曲线y＝ $\frac{k}{x}$ （k＜0）上，连接OA，分别以点O和点A为圆心，大于 $\frac{1}{2}$ OA的长为半径作弧，两弧相交于D，E两点，直线DE交x轴于点B，交y轴于点C（0，3），连接AB.若AB＝1，则k的值为.

查看试题解析

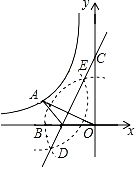
三、解答题

17. 计算： ${(\sqrt{2} - 3)}^{0} + \sqrt{9} - 2 \sin 30^{°} - | - 2 |$ .

查看试题解析
18. 先化简，再求值： $\frac{x^{2} - 2 x}{x^{2} - 1} \div (\frac{x}{x + 1} - \frac{2}{x + 1})$ ，其中 $x$ 是满足不等式组 ${\begin{array}{l} 2 x - 1 < 0 \\ 3 - x ⩾ 0 \end{array}$ 的最大整数.

查看试题解析
19. 节假日期间、某商场组织游戏，主持人请三位家长分别带自己的孩于参加游戏，A、B、C分别表示一位家长，他们的孩子分别对应的是a，b， $c .$ 若主持人分别从三位家长和三位孩子中各选一人参加游戏.

(1)、若已选中家长A，则恰好选中自己孩子的概率是.

(2)、请用画树状图或列表法求出被选中的恰好是同一家庭成员的概率.

查看试题解析
20. 关于x的一次函数 $y_{1} = - 2 x + m$ 和反比例函数 $y_{2} = \frac{n + 1}{x}$ 的图象都经过点 $A (- 2 ， 1)$ .
求：

(1)、一次函数和反比例函数的解析式；

(2)、若一次函数和反比例函数图象的另一个交点B的坐标为 $(\frac{1}{2} ， - 4)$ ，请结合图象直接写出 $y_{1} > y_{2}$ 的x取值范围.

查看试题解析
21. 2020贺岁片《囧妈》提档大年三十网络首播.“乐调查”平台为了全面了解观众对《囧妈》的满意度情况，进行随机抽样调查，分为四个类别：A.非常满意；B.满意；C.基本满意；D.不满意，依据调查数据绘制成图1和图2的统计图（不完整）.

根据以上信息，解答下列问题：

(1)、本次接受调查的观众共有人；

(2)、扇形统计图中，扇形 $C$ 的圆心角度数是；

(3)、请补全条形统计图；

(4)、“乐调查”平台调查了春节期间观看《固妈》的观众约5000人，请估计观众对该电影的满意（ $A$ 、 $B$ 、 $C$ 类视为满意）的人数.

查看试题解析
22. 如图，矩形ABCD中，对角线AC，BD交于点O，以AD，OD为邻边作平行四边形ADOE，连接BE.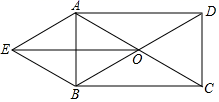

(1)、求证：四边形AOBE是菱形；

(2)、若∠EAO+∠DCO＝180°，DC＝3，求四边形ADOE的面积.

查看试题解析
23. 如图，在三角形ABC中，AB＝10，AC＝BC＝13，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF⊥AC，于点F，交CB的延长线于点E.

(1)、求证：DF是⊙O的切线；

(2)、求cos∠ADF的值.

查看试题解析
24. “全民防控新冠病毒”期间某公司推出一款消毒产品，成本价8元/千克，经过市场调查，该产品的日销售量y（千克）与销售单价x（元/千克）之间满足一次函数关系，该产品的日销售量与销售单价几组对应值如表：

销售单价 $x$ （元/千克）

12

16

20

24

日销售量 $y$ （千克）

220

180

140

$m$

（注：日销售利润 $=$ 日销售量 $\times$ （销售单价 $-$ 成本单价）

(1)、求y关于x的函数解析式（不要求写出x的取值范围）；

(2)、根据以上信息，填空：
① $m =$ 千克；

②当销售价格 $x =$ 元时，日销售利润 $W$ 最大，最大值是元；

(3)、该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象，为了保证捐赠后每天的剩余利润不低于1500元，试确定该产品销售单价的范围.

查看试题解析
25. 随着中国经济的快速发展以及科技水平的飞速提高，中国高铁正迅速崛起，高铁大大缩短了时空距离，改变了人们的出行方式，如图 $A ， B$ 两地被大山阻隔，由 $A$ 地到 $B$ 地需要绕行C地，若打通穿山隧道由 $A$ 地到 $O$ 地，再由 $O$ 地到 $B$ 地可大大缩短路程. $∠ O A C = 45 °$ ， $∠ O B C = 60 °$ ， $∠ A C B = 90 °$ ， $A C = 540$ 公里， $B C = 400$ 公里，求隧道打通后与打通前相比，从 $A$ 地到 $B$ 地的路程将约缩短多少公里？（参考数据： $\sqrt{1.3} \approx 1.7$ ， $\sqrt{2} \approx 1.4$ ， $\sqrt{6} \approx 2.4$ ）

查看试题解析
26. 已知如图1，四边形 $A B C D$ 是正方形， $E ， F$ 分别在边 $B C$ 、 $C D$ 上，且 $∠ E A F = 45 °$ ，我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法.

(1)、在图l中，连接 $E F$ ，为了证明结论“ $E F = B E + D F$ ”，小亮将 $Δ A D F$ 绕点A顺时针旋转 $90 °$ 后解答了这个问题，请按小亮的思路写出证明过程；

(2)、如图2，当 $∠ E A F$ 绕点 $A$ 旋转到图2位置时，试探究 $E F$ 与 $D F$ 、 $B E$ 之间有怎样的数量关系？

(3)、如图3，如果四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = ∠ B C D = 90 °$ ， $∠ E A F {=45}^{\circ}$ ，且 $B C = 7$ ， $D C = 13$ ， $C F = 5$ ，求 $B E$ 的长.

查看试题解析
27. 如图，二次函数y＝﹣x²+2（m﹣2）x+3的图象与x、y轴交于A、B、C三点，其中A（3，0），抛物线的顶点为D.

(1)、求m的值及顶点D的坐标；

(2)、如图1，若动点P在第一象限内的抛物线上，动点N在对称轴1上，当PA⊥NA，且PA＝NA时，求此时点P的坐标；

(3)、如图2，若点Q是二次函数图象上对称轴右侧一点，设点Q到直线BC的距离为d，到抛物线的对称轴的距离为d₁ ，当|d﹣d₁|＝2时，请求出点Q的坐标.

查看试题解析

销售单价 $x$ （元/千克）	12	16	20	24
日销售量 $y$ （千克）	220	180	140	$m$