江苏省徐州市2020年数学中考模拟试卷(5月A卷）

试卷更新日期：2020-07-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 5的倒数是（）

A、 $\frac{1}{5}$ B、 $- 5$ C、 $- \frac{1}{5}$ D、 $5$

查看试题解析
2. 计算﹣3a•（2b），正确的结果是（）

A、﹣6ab B、6ab C、﹣ab D、ab

查看试题解析
3. 如图是一个由5个相同的正方体组成的几何体，它的左视图是（）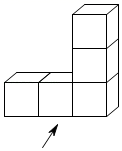

A、 B、 C、 D、

查看试题解析
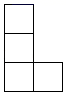4. 如图，D，E分别是△ABC的边AB，AC上的中点，如果△ADE的周长是6，则△ABC的周长是（）

A、24 B、14 C、12 D、6

查看试题解析
5. 生物学家发现了一种病毒，其长度约为 $0.00000032 m m$ ，将数据0. 00000032用科学记数法表示正确的是（）

A、 $3.2 \times 10^{7}$ B、 $3.2 \times 10^{- 7}$ C、 $3.2 \times 10^{8}$ D、 $3.2 \times 10^{- 8}$

查看试题解析
6. 某兴趣小组为了解我市气温变化情况，记录了今年1月份连续6天的最低气温（单位：℃）： $- 7 ， - 4 ， - 2 ， 1 ， - 2 ， 2$ ，关于这组数据，下列结论不正确的是（）

A、平均数是-2 B、中位数是-2 C、众数是-2 D、方差是7

查看试题解析
7. 一元二次方程 $3 x^{2} - 4 x + 1 = 0$ 的根的情况为（）

A、没有实数根 B、只有一个实数根 C、两个相等的实数根 D、两个不相等的实数根

查看试题解析
8. 如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作Rt△ABC，使∠BAC=90°，∠ACB=30°，设点B的横坐标为x，点C的纵坐标为y，能表示y与x的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

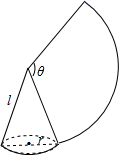
9. 使分式 $\frac{1}{x - 1}$ 有意义的x的取值范围为.

查看试题解析
10. 一元二次方程 $x^{2} - 9 = 0$ 的解是．

查看试题解析
11. 分解因式3a²-3b²= ．

查看试题解析
12. 已知2a﹣3b=7，则8+6b﹣4a= ．

查看试题解析
13. 若正多边形的一个外角是40°，则这个正多边形的边数是.

查看试题解析
14. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形.若圆锥的母线长l为6cm，扇形的圆心角θ＝120°，则该圆锥的侧面积为cm².（结果保留π）

查看试题解析
15. 从﹣1，2，3，﹣6这四个数中任选两数，分别记作m，n，那么点（m，n）在函数y= $\frac{6}{x}$ 图象上的概率是．

查看试题解析
16. 已知点A是直线y=x+1上一点，其横坐标为﹣ $\frac{1}{2}$ ，若点B与点A关于y轴对称，则点B的坐标为．

查看试题解析
17. 如图，将▱ABCD沿EF对折，使点A落在点C处，若∠A＝60°，AD＝4，AB＝8，则AE的长为.

查看试题解析
18. 已知抛物线y=x²+2x﹣3与x轴交于A，B两点（点A在点B的左侧），将这条抛物线向右平移m（m＞0）个单位长度，平移后的抛物线与x轴交于C，D两点（点C在点D的左侧），若B，C是线段AD的三等分点，则m的值为.

查看试题解析

三、解答题

19. 计算：

(1)、（﹣2017）⁰﹣（ $\frac{1}{3}$ ）^﹣¹+ $\sqrt{9}$ ；

(2)、化简：（ $\frac{a^{2}}{b}$ ﹣a）÷ $\frac{a^{2} - b^{2}}{b}$ .

查看试题解析
20.

(1)、解方程： $\frac{2 x}{x - 2}$ ＝1﹣ $\frac{1}{2 - x}$ ；

(2)、解不等式组： ${\begin{array}{l} x - 1 \geq 2 x \\ \frac{x}{2} + 3 < - 2 \end{array}$ .

查看试题解析
21. 端午节当天，小明带了四个粽子（除味道不同外，其它均相同），其中两个是大枣味的，另外两个是火腿味的，准备按数量平均分给小红和小刚两个好朋友．

(1)、请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性．

(2)、请你计算小红拿到的两个粽子刚好是同一味道的概率．

查看试题解析
22. 在“宏扬传统文化，打造书香校园”活动中，学校计划开展四项活动：“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”，要求每位同学必须且只能参加其中一项活动，学校为了了解学生的意愿，随机调查了部分学生，结果统计如下：

(1)、如图，希望参加活动C占20%，希望参加活动B占15%，则被调查的总人数为 ▲ 人，扇形统计图中，希望参加活动D所占圆心角为 ▲ 度，根据题中信息补全条形统计图.

(2)、学校现有800名学生，请根据图中信息，估算全校学生希望参加活动A有多少人？

查看试题解析
23. 如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，连接CD．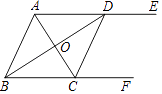

(1)、求证：四边形ABCD是菱形；

(2)、若∠ADB=30°，BD=6，求AD的长．

查看试题解析
24. 如图，△ABC内接于⊙O，∠B=60⁰ ， CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．

(1)、求证：PA是⊙O的切线；

(2)、若PD= $\sqrt{3}$ ，求⊙O的直径．

查看试题解析
25.
如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m²？

查看试题解析
26. 如图，一艘船以每小时30海里的速度向北偏东75°方向航行，在点 $A$ 处测得码头 $C$ 的船的东北方向，航行40分钟后到达 $B$ 处，这时码头 $C$ 恰好在船的正北方向，在船不改变航向的情况下，求出船在航行过程中与码头 $C$ 的最近距离.（结果精确的0.1海里，参考数据 $\sqrt{2} \approx {1.41}_{：} \sqrt{3} \approx 1.73$ ）

查看试题解析
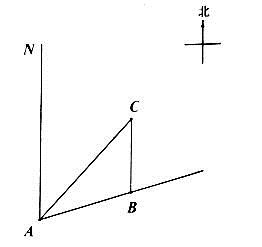27. 如图1和图2，在△ABC中，AB＝13，BC＝14， $\frac{B H}{A B} = \frac{5}{13}$ .

(1)、探究：如图1，AH⊥BC于点H，则AH＝， AC＝， △ABC的面积 $S_{Δ A B C}$ ＝.

(2)、拓展：如图2，点D在AC上（可与点A、C重合），分别过点A、C作直线BD的垂线，垂足为E、F，设BD＝x，AE＝m，CF＝n，（当点D与A重合时，我们认为 $S_{Δ A B D}$ ＝0）.
①用含x、m或n的代数式表示 $S_{Δ A B D}$ 及 $S_{Δ C B D}$ ；

②求(m+n)与x的函数关系式，并求(m+n)的最大值和最小值；

(3)、对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围.
发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值.

查看试题解析
28. 如图，抛物线y=﹣x²+bx+c和直线y=x+1交于A，B两点，点A在x轴上，点B在直线x=3上，直线x=3与x轴交于点C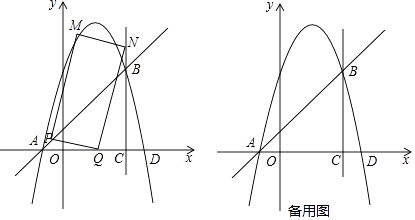

(1)、求抛物线的解析式；

(2)、点P从点A出发，以每秒 $\sqrt{2}$ 个单位长度的速度沿线段AB向点B运动，点Q从点C出发，以每秒2个单位长度的速度沿线段CA向点A运动，点P，Q同时出发，当其中一点到达终点时，另一个点也随之停止运动，设运动时间为t秒（t＞0）．以PQ为边作矩形PQNM，使点N在直线x=3上．
①当t为何值时，矩形PQNM的面积最小？并求出最小面积；
②直接写出当t为何值时，恰好有矩形PQNM的顶点落在抛物线上．

查看试题解析