山东省泰安市高新区2019-2020学年八年级下学期数学期末考试试卷（五四学制）
试卷更新日期：2020-07-22 类型：期末考试
一、选择题(本大题共12小题，每小题4分)
-
1. 下列二次根式中，与 是同类二次根式的是（ ）A、 B、 C、 D、2. 如图，D、E分别为AB、AC上的两点，DE∥BC，AE=2CE，AB=9，则AD的长为（ ）
A、6 B、5 C、4 D、33. 下列运算正确的是（ ）A、2+ =2 B、 C、 D、3 - =34. a是方程x²+x-1=0的一个根，则代数式-2a²-2a+2020的值是（ ）A、2018 B、2019 C、2020 D、20215. 如图，△ABC中，D、E分别是BC、AC边上一点，F是AD、BE的交点，CE=2AE，BF=EF，EN∥BC交AD于N，若BD=2，则CD长度为（ ）
A、6 B、7 C、8 D、96. 若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根，则k的取值范围是（ ）A、k> 且k≠1 B、k> C、k≥ 且k≠1 D、k<7. 如图，在平行四边行ABCD中，M，N是BD上两点，BM=DN，连接AM，MC，CN，NA，添加一个条件，使四边形AMCN是菱形，这个条件是（ ）
A、OM= AC B、MB=MO C、BD⊥AC D、∠AMB=∠CND8. 如图，以点O为位似中心，把△ABC中放大到原来的2倍得到△A'B'C'。以下说法中错误的是（ ）
A、△ABC∽△A'B'C' B、点C，O，C'三点在同一条直线上 C、AO：AA'=1：2 D、AB∥A'B'9. 如图，矩形ABCD的边长AD=8，AB=6，E为AB的中点，AC分别与'DE，DB相交于点M，N，则MN的长为（ ）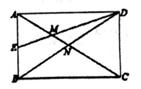
A、1 B、2 C、 D、10. 学生会组织周末爱心义卖活动，义卖所得利润将全部捐献给希望工程，活动选在一块长20米、宽14米的矩形空地上．如图，空地被划分出6个矩形区域，分别摆放不同类别的商品，区域之间用宽度相等的小路隔开，已知每个区域的面积均为32平方米，小路的宽应为多少米？设小路的宽为x米，依据题意列方程得（ ）
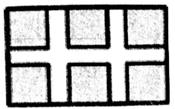A、(20-2x)(14-x)=32×6 B、(20-x)(14-2x)=32×6 C、(20-2x)(14-x)=20×14 D、(20-2x)(14-x)+2x2=32×611. 如图，在正方形ABCD中，点O是对角线AC、BD的交点，过点O作射线OM、ON分别交BC、CD于点E、F，且∠EOF=90°，OC、EF交于点G．给出下列结论：①△COE≌△DOF；②△OGE∽△FGC；③四边形CEOF的面积为正方形ABCD面积的 ；④DF2+BE2=OG·OC。其中正确的是（ ）
A、1个 B、2个 C、3个 D、4个12. 如图，CE是平行四边形ABCD的边AB的垂直平分线，垂足为点O，CE与DA的延长线交于点E．连接AC，BE，DO，DO与AC交于点F，则下列结论：①四边形ACBE是菱形；②∠ACD=∠BAE；③AF：BE=2：3；④S四边形AFOE：S△COD=2：3；以上四个结论中所有正确的结论有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共6小题，满分24分。)
-
13. 若 在实数范围内有意义，则x的取值范围是。14. 把一个长方形按如图方式划分成三个全等的小长方形，每一个小长方形与原长方形相似，若小长方形的宽为2，则原长方形的宽x为。
15. 关于x的方程x(x-1)+3(x-1)=0的解是。16. 若3<a<5，则 +|5-a|=。17. 如图，在△ABC与△AED中， ，添加一个条件，使△ABC与△AED相似，这个条件可以是。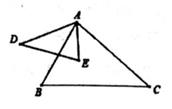
18. 我国古代数学著作《九章算术》中记载：“今有方不知大小，各开中门，出北门四十步有木，出西门八百一十步见木，问：邑方几何？”译文：如图，一座正方形城池北、西边正中A、C处各开一道门，从点A往正北方向走40步刚好有一棵树位于点B处，若从点C往正西方向走810步到达点D处时正好看到此树，则正方形城池的边长为步。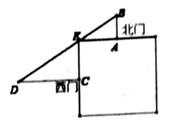
三、解答题(共7小题，满分78分。)
-
19. 计算(1)、(2)、( -5)（6+ ）-(3- )+( )20. 用指定的方法解方程：(1)、2x2-5x+3=0(用公式法解方程)(2)、3x²-5=6x(用配方法解方程)21. 如图，在菱形ABCD中，AE⊥AD交BD于点E，CF⊥BC交BD于点F。
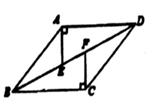(1)、求证：△ADE≌△CBF；(2)、连接AF、CE，判断四边形AECF的形状，并说明理由。22. 如图，在△ABC中，BC的垂直平分线分别交BC、AC于点D、E，BE交AD于点F，AB=AD。
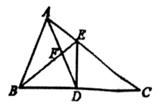(1)、判断△FDB与△ABC是否相似， 并说明理由；(2)、若AF=4，求AB的长。23. 在全国人民的共同努力下，新冠疫情防控得到有效控制，复工复产后，某玩具经销商在销售中发现：某款进价为每个30元的玩具，若以每个40元销售，一个月能售出400个，销售单价每涨1元，月销售量就减少10个，请回答以下问题：(1)、若上涨a元，则销量为个。(2)、若月销售利润定为6000元，且尽可能让利消费者，销售单价应定为多少元？(3)、由于资金问题，月销售成本不超过9000元(没有库存积压)，销售单价至少定为多少元？
