山东省泰安高新区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-07-22 类型:期末考试
一、选择题(本大题共12小题,每小题4分。)
-
1. 二元一次方程组 的解为( )A、 B、 C、 D、2. 一个布袋里装有4个红球、1个黄球和5个白球,除颜色外其它都相同。搅匀后任意摸出一个球,是红球的概率为( )A、 B、 C、 D、3. 若a>b,则下列不等式不成立的是( )A、a-2>b-2 B、5-a>5-b C、7a>7b D、4. 如图,在△ABC中,∠BAC=70°,∠C=80°,AD平分∠BAC交BC于点D,点E是AC上一点,∠ADE=∠B,则∠CDE的度数为( )
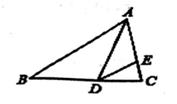 A、15° B、25° C、30° D、35°5. 若 ,是关于x,y的方程组 的解,则a+b的值是( )A、5 B、3 C、-1 D、46. 不等式2x-1≤3的解集在数轴上表示正确的是( )A、
A、15° B、25° C、30° D、35°5. 若 ,是关于x,y的方程组 的解,则a+b的值是( )A、5 B、3 C、-1 D、46. 不等式2x-1≤3的解集在数轴上表示正确的是( )A、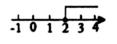 B、
B、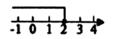 C、
C、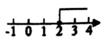 D、
D、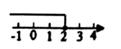 7. 如图,在△ABC中,BC=8,AB的垂直平分线分别交AB,AC于点D,E。若△BCE的周长为17,则AC的长为( )
7. 如图,在△ABC中,BC=8,AB的垂直平分线分别交AB,AC于点D,E。若△BCE的周长为17,则AC的长为( ) A、8 B、9 C、15 D、178. 如图,在△ABC中,∠C=90°,AD平分∠BAC,且DE⊥AB于E,DE=5,BC=11,则BD的长为( )
A、8 B、9 C、15 D、178. 如图,在△ABC中,∠C=90°,AD平分∠BAC,且DE⊥AB于E,DE=5,BC=11,则BD的长为( )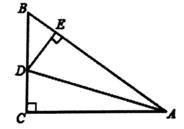 A、5 B、6 C、7 D、89. 如图所示,BC,DE交于点O,∠B=∠E,再补充一个条件,使AB∥DE。下列条件:①BC∥EF;②∠DOC=∠B;③∠COE+∠E=180°;④∠BOE=∠E;⑤∠BOD+∠E=180°。其中,可以补充的这个条件可以有( )
A、5 B、6 C、7 D、89. 如图所示,BC,DE交于点O,∠B=∠E,再补充一个条件,使AB∥DE。下列条件:①BC∥EF;②∠DOC=∠B;③∠COE+∠E=180°;④∠BOE=∠E;⑤∠BOD+∠E=180°。其中,可以补充的这个条件可以有( )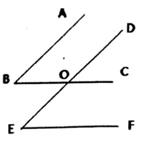 A、2个 B、3个 C、4个 D、5个10. 若关于x的不等式组 有解,则m的取值范围是( )A、m<5 B、m>5 C、m≤5 D、m≥511. 我国古代数学作《九章算术》有一道关于买田的问题:“今有善田一亩,价三百;恶田一亩,价五十。今并买顷,价钱一万,问善田恶田各几何?”其意思是“好田300钱一亩,坏田50一亩,合买好田、坏田100亩,共需10000钱,问好田、坏田各买了多少亩?”若设好田买了x亩,坏田买了y亩。则列方程组为( )A、 B、 C、 D、12. 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,现将Rt△ABC沿BD进行翻折,使点A刚好落在BC上,则CD的长为( )
A、2个 B、3个 C、4个 D、5个10. 若关于x的不等式组 有解,则m的取值范围是( )A、m<5 B、m>5 C、m≤5 D、m≥511. 我国古代数学作《九章算术》有一道关于买田的问题:“今有善田一亩,价三百;恶田一亩,价五十。今并买顷,价钱一万,问善田恶田各几何?”其意思是“好田300钱一亩,坏田50一亩,合买好田、坏田100亩,共需10000钱,问好田、坏田各买了多少亩?”若设好田买了x亩,坏田买了y亩。则列方程组为( )A、 B、 C、 D、12. 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,现将Rt△ABC沿BD进行翻折,使点A刚好落在BC上,则CD的长为( ) A、10 B、5 C、4 D、3
A、10 B、5 C、4 D、3二、填空题(本大题共6小题,满分24分。每小题4分)
-
13. 把命题“对顶角相等”改写成“如果……,那么……”的形式:.14. 等腰三角形的顶角是40°,则底角的度数为°。15. 如图,AB∥CD,AB=AC,∠1=30°,则∠ACE的度数是°。
 16. 如图,直线l1:y=x+2与直线l2:y=ax+c相交于点P(m,3)。则关于x,y的二元一次方程组 的解是 。
16. 如图,直线l1:y=x+2与直线l2:y=ax+c相交于点P(m,3)。则关于x,y的二元一次方程组 的解是 。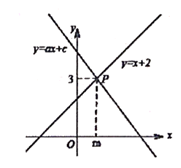 17. 如图,AB=DE,AB∥DE,补充一个条件,能使△ABC≌△DEF的条件是。
17. 如图,AB=DE,AB∥DE,补充一个条件,能使△ABC≌△DEF的条件是。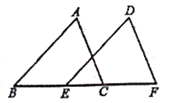 18. 某次知识竞赛共有20道题,每道题答对得10分,答错或不答扣5分,小明得分要超过110分,他至少要答对几道题?若设小明答对x道题,则依据题意得 。(只列不解)
18. 某次知识竞赛共有20道题,每道题答对得10分,答错或不答扣5分,小明得分要超过110分,他至少要答对几道题?若设小明答对x道题,则依据题意得 。(只列不解)三、解答题(共7小题,满分78分.)
-
19. 用指定的方法解下列方程组:(1)、 (代入消元法)(2)、 (加减消元法)20. 解关于x的不等式组 ,并把解集表示在数轴上。21. 某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图,并规定:顾客每购买200元的商品就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以分别获得100元、50元,20元的购物券,(转盘被等分成20个扇形),若甲顾客购物220元。
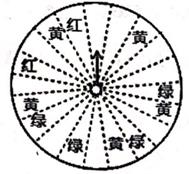 (1)、他获得100元购物券的概率是多少?(2)、他获得购物券的概率是多少?(3)、商场若将获得20元购物券的概率变为 ,则转盘的颜色部分怎样修改?22. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,2),与x轴交于点C(1,0),与y=2x-5相交于点P,直线y=2x-5与y轴交于点B。
(1)、他获得100元购物券的概率是多少?(2)、他获得购物券的概率是多少?(3)、商场若将获得20元购物券的概率变为 ,则转盘的颜色部分怎样修改?22. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,2),与x轴交于点C(1,0),与y=2x-5相交于点P,直线y=2x-5与y轴交于点B。 (1)、求一次函数y=kx+b的函数解析式;(2)、求△APB的面积;(3)、依据图像直接写出kx+b>2x+5时x的取值范围。23. 如图,BE平分∠ABC,CE平分∠ACD,BE、CE交于点E,∠ABC=∠ACE。
(1)、求一次函数y=kx+b的函数解析式;(2)、求△APB的面积;(3)、依据图像直接写出kx+b>2x+5时x的取值范围。23. 如图,BE平分∠ABC,CE平分∠ACD,BE、CE交于点E,∠ABC=∠ACE。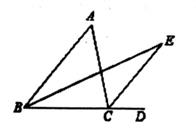 (1)、求证:AB∥CE;(2)、若∠A=40°,求∠E的度数。24. 如图,点D,E分别在等边△ABC的两边AB,AC上,AD=BE,BD,CE交于点P。CF⊥BD于点F。
(1)、求证:AB∥CE;(2)、若∠A=40°,求∠E的度数。24. 如图,点D,E分别在等边△ABC的两边AB,AC上,AD=BE,BD,CE交于点P。CF⊥BD于点F。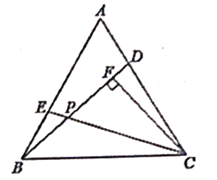 (1)、判断线段BD,CE的数量关系,并证明;(2)、求∠DPC的度数;(3)、若CP=10,求PF的长。25. 某体育用品商店购进了足球和排球,进价和售价如下表:
(1)、判断线段BD,CE的数量关系,并证明;(2)、求∠DPC的度数;(3)、若CP=10,求PF的长。25. 某体育用品商店购进了足球和排球,进价和售价如下表:足球
排球
进价(元/个)
80
50
售价(元/个)
95
60
(1)、若购进足球和排球共20个,一共花费1360元,求购进足球和排球各多少个?(2)、在(1)的条件下,全部售完后,商店共获利多少元?(3)、若商店一次性共购进50个球,想获得不低于600元的利润,足球至少购进多少个?