山东省滨州市阳信县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期：2020-07-22 类型：期末考试
一、选择题：
-
1. 满足下列条件的△ABC中，不是直角三角形的是（ ）A、b²=c²-a² B、a：b：c=3：4：5 C、∠C=∠A-∠B D、∠A：∠B：∠C=3：4：52. 下列说法错误的是（ ）A、圆周长C是半径r的正比例函数 B、对角线相等的四边形是矩形 C、菱形的对角线互相垂直平分 D、方差越大，波动越大3. 如图，在四边形ABCD中，下列条件不能判定四边形ABCD是平行四边形的是（ ）
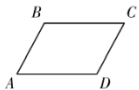A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AD∥BC，AB=DC D、AB∥DC，AB=DC4. 已知n是方程x²-2x-1=0的一个根，则3n²-6n-7的值为（ ）A、-5 B、-4 C、-3 D、-25. 用配方法解一元二次方程2x²-x-1=0时，配方正确的是（ ）A、 B、 C、 D、6. 点A(x1 ， y1)、B(x2 ， y2)都在直线y=kx+2(k<0)上，且x1<x2 ， 则y1、y2的大小关系是（ ）A、y1=y2 B、y1<y2 C、y1>y2 D、无法判断7. 疫情无情人有情，爱心捐款传真情.新型冠状病毒感染的肺炎疫情期间，某班学生积极参加献爱心活动，该班50名学生的捐款统计情况如下表：金额/元
5
10
20
50
100
人数
6
17
14
8
5
则他们捐款金额的平均数和中位数分别是（ ）
A、 B、 C、 D、8. 已知一次函数y=kx+b(k，b是常数，且k≠0)，x与y的部分对应值如下表所示，那么不等式kx+b<0的解集是（ ）x
-2
-1
0
1
2
3
y
3
2
1
0
-1
-2
A、x<0 B、x>0 C、x<1 D、x>19. 学校图书馆去年年底有图书5万册，预计到明年年底增加到7.2万册。设这两年的平均增长率为x，则下列方程正确的是（ ）A、5(1+x)=7.2 B、5(1+2x)=7.5 C、5(1+x)²=7.2 D、5(1+x)+5(1+x)²=7.210. 若关于x的一元二次方程x²-2x+kb+1=0有两个不相等的实数根，则一次函数y=kx+b的图象可能是（ ）A、
B、
C、
D、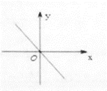
11. 如图，正方形 和正方形 中，点 在 上， ， ， 是 的中点，那么 的长是（ ）
A、2 B、 C、 D、12. 如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，P是斜边BC上一动点，PE⊥AB于点E，PF⊥AC于点F，EF与AP相交于点O，则OF的最小值为（ ）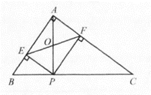
A、4.8 B、1.2 C、3.6 D、2.4二、填空题
-
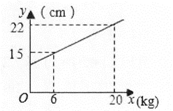
13. 在函数)y= 中，自变量x的取值范围是。14. 已知，一元二次方程的两根是0，2，则这个一元二次方程为。15. 如果样本数据3,6,a,4,2的平均数为4，则这个样本的方差为.16. 如图，弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数，则弹簧不挂物体时的长度为 cm。
17. 如图，在矩形ABCD中，AC、BD交于点O，DE⊥AC于点E，若∠AOD=110°，则∠CDE=°。
18. 如图，已知一次函数y=2x+b和y=kx-3(k≠0)的图象交于点P，则二元一次方程组 的解是。
19. 菱形ABCD的两条对角线AC，BD相交于点O，E是AB的中点，若AC=12，菱形ABCD的面积为96，则OE长为。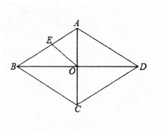
20. 如图，在平面直角坐标系中，长方形OACB的顶点O在坐标原点，顶点A，B分别在x轴，y轴的正半轴上，OA=3，OB=4，D为边OB的中点，E是边OA上的一个动点，当△CDE的周长最小时，点E的坐标为。
三、解答题：本大题共6个小题，满分74分。
-
21. 按要求解下列方程．(1)、3x²+x-5=0(公式法)(2)、(x+2)²-4(x-3)²=0(因式分解法)22. 已知关于x的一元二次方程：x²-(m-3)x-m=0。(1)、试判断原方程根的情况；(2)、若方程的两根为x1 ， x2 ， 且(x1-3)(x2-3)=10，求m的值。23. 笔直的河流一侧有一旅游地C，河边有两个漂流点A、B，其中AB=AC，由于某种原因，由C到A的路现在已经不通，为方便游客，决定在河边新建一个漂流点H(A，H，B在一条直线上)，并新修一条路CH，测得BC=5千米，CH=4千米，BH=3千米，
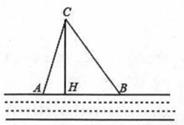(1)、问CH是否为从旅游地C到河的最近的路线？请通过计算加以说明；(2)、求原来路线AC的长。24. 如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连结AE，CF。
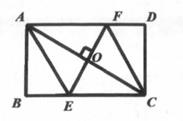(1)、求证：四边形AECF是菱形；(2)、若AB= ，∠DCF=30°，求四边形AECF的面积。(结果保留根号)。25. 某网店销售某款童装，每件售价60元，每星期可卖300件，为尽快减少库存，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件。已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件。(1)、求y与x之间的函数关系式；(2)、当每件售价定为多少元时，该商店每天的销售利润为6480元？26. 如图，在平面直角坐标系中，O为原点，已知直线y= x+4与x轴交于点A，与y轴交于点B。(1)、点A的坐标为 ， 点B的坐标为。(2)、)如图①，若点M(x，y)在线段AB上运动(不与端点A、B重合)，连接OM，设△AOM的面积为S，写出S关于x的函数解析式，并写出自变量x的取值范围；(3)、如图②，若四边形OADC是菱形，求菱形对角线OD的长。