山东省聊城市莘县2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-22 类型:期末考试
一、选择题(本题共12个小题,每小题3分,共36分)
-
1. 下列说法中不正确的是( )A、在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直 B、从直线外一点到这条直线的垂线段叫做点到直线的距离 C、一条直线的垂线可以画无数条 D、连接直线外一点与直线上各点的所有线段中,垂线段最短2. 下列运算正确的是( )A、2a3·a4=2a12 B、(-3a²)3=-9a6 C、a2÷a× =a2 D、a·a3+a²·a²=2a43. 下列方程组中不是二元一次方程组的是( ) .A、 B、 C、 D、4. 如图所示,下列说法:①∠1与∠C是同位角;②∠2与∠C是内错角;③∠3与∠B是同旁内角;④∠3与∠C是同旁内角,其中正确的是( )
 A、①②③ B、②③④ C、①③④ D、①②④5. 在等式a3·a²( )=a11中,括号里填入的代数式应当是( )A、a2 B、a8 C、a6 D、a36. 如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )
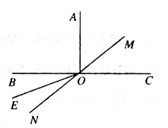
A、①②③ B、②③④ C、①③④ D、①②④5. 在等式a3·a²( )=a11中,括号里填入的代数式应当是( )A、a2 B、a8 C、a6 D、a36. 如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )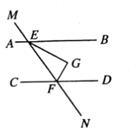 A、20° B、25° C、35° D、40°7. 如果3x3m-2n-4yn-m+12=0是关于x、y的二元一次方程,那么m、n的值分别为( )A、m=2,n=3 B、m=2,n=1 C、m=-1,n=2 D、m=3,n=48. 如图,∠AOC和∠BOC互补,∠AOB=α , OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON的度数( )
A、20° B、25° C、35° D、40°7. 如果3x3m-2n-4yn-m+12=0是关于x、y的二元一次方程,那么m、n的值分别为( )A、m=2,n=3 B、m=2,n=1 C、m=-1,n=2 D、m=3,n=48. 如图,∠AOC和∠BOC互补,∠AOB=α , OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON的度数( )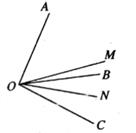 A、180°-2α B、 α C、90°+ α D、90°- α9. 如果方程组 的解为 ,那么“□”和“△”所表示的数分别是( )A、14,4 B、11,1 C、9,-1 D、6,-410. 如图,将一副直角三角尺叠放在一起,使直角顶点重合与点O,若∠DOC=28°,则∠AOB的度数为( )
A、180°-2α B、 α C、90°+ α D、90°- α9. 如果方程组 的解为 ,那么“□”和“△”所表示的数分别是( )A、14,4 B、11,1 C、9,-1 D、6,-410. 如图,将一副直角三角尺叠放在一起,使直角顶点重合与点O,若∠DOC=28°,则∠AOB的度数为( )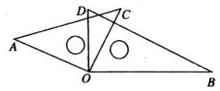 A、62° B、152° C、118° D、无法确定11. 已知方程组 中的x,y互为相反数,则n的值为( )A、2 B、-2 C、0 D、412. 计算( )2020x( )2021=( )A、-1 B、 C、1 D、
A、62° B、152° C、118° D、无法确定11. 已知方程组 中的x,y互为相反数,则n的值为( )A、2 B、-2 C、0 D、412. 计算( )2020x( )2021=( )A、-1 B、 C、1 D、二、填空题(本题共5个小题,每小题3分,共15分)
-
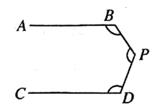
13. 如图,AB∥CD,则∠B+∠D+∠P=。
 14. 已知5m=2,5n=3,则53m+n-1的值为 。15. 若关于x,y的二元一次方程组 的解也是二元一次方程2x-y=-7的解,则k的值是。16. 如图OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD的度数是度。
14. 已知5m=2,5n=3,则53m+n-1的值为 。15. 若关于x,y的二元一次方程组 的解也是二元一次方程2x-y=-7的解,则k的值是。16. 如图OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD的度数是度。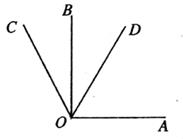 17. 观察下列各式
17. 观察下列各式(x-1)(x+1)=x²-1
(x-1)(x²+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
……
你能否由此归纳出一般性规律:(x-1)(x2019+x2018+……+x+1)=。
三、解答题(本题共8个小题,共69分,)
-
18. 计算:(1)、-12020+(π-5)0-( )-2-|-2|(2)、3(x2)3·x3-(x3)3+(-2x)²·x9÷x²(3)、先化简,再求值[(2x-y)(2x-y)+(2x+y)(2x-y)+4xy] ÷2x,其中x=-4,y= 。19. 解下列方程组:(1)、(2)、20. 如图所示,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM的度数。
 21. 甲、乙两名同学在解方程组 时,甲解题时看错了m,解得 ;乙解题时看错了n,解得 。请你根据以上两种结果,求出原方程组的正确解。22. 甲乙两人共同做一道整式乘法的计算题(2x+a)(3x+b),由于甲抄错了第1个多项式中a的符号,得到的结果为6x2+7x+2,由于乙漏抄了第2个多项式中x的系数,得到的结果为2x2+3x-2,请你计算出a、b的值各是多少,并写出正确的算式及结果。23. 如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC。
21. 甲、乙两名同学在解方程组 时,甲解题时看错了m,解得 ;乙解题时看错了n,解得 。请你根据以上两种结果,求出原方程组的正确解。22. 甲乙两人共同做一道整式乘法的计算题(2x+a)(3x+b),由于甲抄错了第1个多项式中a的符号,得到的结果为6x2+7x+2,由于乙漏抄了第2个多项式中x的系数,得到的结果为2x2+3x-2,请你计算出a、b的值各是多少,并写出正确的算式及结果。23. 如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC。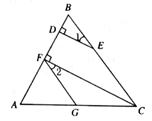 24. 目前节能灯在城市已基本普及,今年某省面向农村地区推广,为响应号召,某商场用3300元购进节能灯100只,这两种节能灯的进价、售价如表:
24. 目前节能灯在城市已基本普及,今年某省面向农村地区推广,为响应号召,某商场用3300元购进节能灯100只,这两种节能灯的进价、售价如表:进价 元 只
售价 元 只
甲种节能灯
30
40
乙种节能灯
35
50
(1)、求甲、乙两种节能灯各进多少只?(2)、全部售完100只节能灯后,该商场获利多少元?25. 直线AB、CD被直线EF所截,AB∥CD,点P是平面内一动点。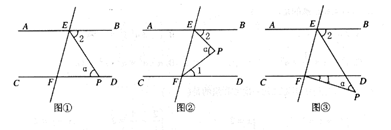 (1)、若点P在直线CD上,如图①,∠α=50°,则∠2=°。(2)、若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;(3)、若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由。
(1)、若点P在直线CD上,如图①,∠α=50°,则∠2=°。(2)、若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;(3)、若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由。