江苏省无锡市梁溪区2020年数学中考模拟试卷

试卷更新日期：2020-07-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 3的绝对值是（）

A、 3 B、－3 C、±3 D、 $\sqrt{3}$

查看试题解析
2. 下列计算中，正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(a^{2})}^{3} = a^{6}$ C、 $a^{3} + a^{3} = a^{6}$ D、 $2 a \cdot 3 a = 6 a$

查看试题解析
3. 若分式 $\frac{x}{x - 2}$ 有意义，则实数x的取值范围是（）

A、 $x > 0$ B、 $x > 2$ C、 $x \neq 0$ D、 $x \neq 2$

查看试题解析
4. 若关于x的方程 $x^{2} + p x + q = 0$ 有两个不相等的实数根，则下列结论正确的是（）

A、 $p^{2} - 4 q > 0$ B、 $p^{2} - 4 q \geq 0$ C、 $p^{2} + 4 q > 0$ D、 $p^{2} + 4 q \geq 0$

查看试题解析
5. 一组数据：3，4，4，4，5.若拿掉一个数据4，则发生变化的统计量是（）

A、极差 B、方差 C、中位数 D、众数

查看试题解析
6. 一个几何体的主视图、左视图、俯视图都是圆形，这个几何体可能是（）

A、圆柱 B、圆锥 C、球 D、半球

查看试题解析
7. 如图，点 $E$ 在四边形 $A B C D$ 的 $C D$ 边的延长线上，若 $∠ A D E = 120 °$ ，则 $∠ A + ∠ B + ∠ C$ 的度数为（）

A、 $240 °$ B、 $260 °$ C、 $300 °$ D、 $320 °$

查看试题解析
8. 若二次函数 $y = a {(x - 1)}^{2} + k$ 的图象与 $x$ 轴交于点 $(- 2, 0)$ ，则图象与x轴的另一个交点为（）

A、 $(0, 0)$ B、 $(2, 0)$ C、 $(3, 0)$ D、 $(4, 0)$

查看试题解析
9. 如图， $Δ A B C$ 中， $A B = 8$ ， $A C = 6$ ， $∠ A = 90 °$ ，点 $D$ 在 $Δ A B C$ 内，且 $D B$ 平分 $∠ A B C$ ， $D C$ 平分 $∠ A C B$ ，过点D作直线 $P Q$ ，分别交 $A B$ 、 $A C$ 于点P、Q，若 $Δ A P Q$ 与 $Δ A B C$ 相似，则线段 $P Q$ 的长为（）

A、5 B、 $\frac{35}{6}$ C、5或 $\frac{35}{6}$ D、6

查看试题解析
10. 如图，动点M从（0，3）出发，沿y轴以每秒1个单位长度的速度向下移动，同时动点 $N$ 从 $(4 ， 0)$ 出发，沿 $x$ 轴以每秒2个单位长度的速度向右移动，当点M移动到O点时，点M、N同时停止移动.点 $P$ 在第一象限内，在M、N移动过程中，始终有 $P M ⊥ P N$ ，且 $P M = P N$ .则在整个移动过程中，点P移动的路径长为（）

A、 $\frac{3}{2} \sqrt{2}$ B、 $\frac{3}{2} \sqrt{3}$ C、 $\sqrt{5}$ D、 $\frac{2}{3} \sqrt{5}$

查看试题解析

二、填空题

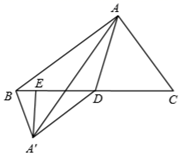
11. 5的算术平方根是.

查看试题解析
12. 无锡和江阴之间的市域轨道交通 $S1$ 号线一期工程线路全长约 $30400 m$ ，数据30400用科学记数法表示为.

查看试题解析
13. 已知代数式 $3 a^{2} b$ ，请写出一个它的同类项：.

查看试题解析
14. 一个菱形的两条对角线长分别为 $4 cm$ 和 $5 cm$ ，则这个菱形的面积是 ${cm}^{2}$ .

查看试题解析
15. 已知圆锥的高为 $12 cm$ ，它的底面直径为 $10 cm$ ，则这个圆锥的母线长为 $cm$ .

查看试题解析
16. 已知反比例函数 $y = \frac{k - 1}{x}$ 的图象经过点 $(2, - 3)$ ，则 $k$ 的值为.

查看试题解析
17. 在平面直角坐标系中，已知 $A (- 1 ， - 1)$ 、 $B (0 ， 2)$ 、 $C (3 ， 3)$ 都在 $⊙ M$ 上，则圆心 $M$ 的坐标为.

查看试题解析
18. 如图， $Δ A B C$ 中， $A B = 8$ ， $B C = 6$ ， $A C = 4$ ，以边 $A B$ 为斜边在 $Δ A B C$ 形外作 $Rt Δ A D B$ ，使得 $∠ A D B = 90 °$ ，连接 $C D$ ，则 $C D$ 的最大值为.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(\frac{1}{2})}^{- 1} + \sqrt{12} - \tan 60 °$ ；

(2)、 ${(a + 3)}^{2} - (a + 2) (a - 1)$ .

查看试题解析
20.

(1)、分解因式： $x^{3} - 4 x$ ；

(2)、解方程： $\frac{5}{x - 1} = \frac{3}{x + 3}$ .

查看试题解析
21. 如图，四边形 $A B C D$ 是平行四边形，E、F分别是 $A D$ 、 $B C$ 的中点， $E F$ 与 $B D$ 交于点G.求证： $E F$ 与 $B D$ 互相平分.

查看试题解析
22. 小亮和小伟一起参加象棋比赛，他们所在的小组共有5名选手.抽签袋里有2红2黑1白共5个小球，摸到同色的成为首轮对手，摸到白球的首轮轮空.现在小组其他3名选手首先依次各摸走一个小球，小亮看到第1个选手摸走的是红球，他对小伟说根据这3名选手的摸球结果我已经知道咱俩恰好首轮对阵的概率了.请你求这个概率.（请用“画树状图”或“列表”等方法写出分析过程）

查看试题解析

23. 某初中为了了解学生的视力情况，从三个年级随机抽取了部分学生进行调查，并制作了下面的统计表和统计图.

各年级抽查学生视力各等第人数分布统计表

	优秀	良好	合格	不合格
七年级	$a$	20	22	23
八年级	11	17	13	19
九年级	8	$b$	11	25

(1)、在统计表中，

a =

，

b =

；

(2)、在扇形统计图中，八年级所对应的扇形圆心角为°；

(3)、若该校三个年级共有1800名学生，试估计该校学生视力等第不合格的人数.

查看试题解析

24. 如图，在 $⊙ O$ 中， $A B$ 为直径，点C、D都在 $⊙ O$ 上，且 $B D$ 平分 $∠ A B C$ ，过点D作 $D E ⊥ B C$ ，交 $B C$ 的延长线于点E.

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、若 $B C = \sqrt{3}$ ， $C E = 1$ ，求 $⊙ O$ 的直径.

查看试题解析
25.

(1)、如图1，点 $A$ 在 $⊙ O$ 上，请在图中用直尺（不含刻度）和圆规作等边三角形 $A B C$ ，使得点B、C都在 $⊙ O$ 上.

(2)、已知矩形 $A B C D$ 中， $A B = 4$ ， $B C = m$ .
①如图2，当 $m = 4$ 时，请在图中用直尺（不含刻度）和圆规作等边三角形 $A E F$ ，使得点 $E$ 在边 $B C$ 上，点 $F$ 在边 $C D$ 上；

②若在该矩形中总能作出符合①中要求的等边三角形 $A E F$ ，请直接写出 $m$ 的取值范围.

查看试题解析

26. 小明去超市采购防疫物品，超市提供下表所示A、B两种套餐，小明决定购买50份

A

套餐.超市为了促进消费，给出两种优惠方式，方式一：现金支付总额每满700元立减200元；方式二：现金支付总额每满600元送300元现金券，现金券可等同现金使用，但是使用现金券的总额不能超过应付总金额.

套餐类别	一次性防护口罩	免洗洗手液	套餐价格
A	2包	1瓶	71元
B	1包	2瓶	67元

(1)、求一次性防护口罩和免洗洗手液各自的单价；

(2)、小明觉得优惠方式二比方式一的优惠力度更大，他计划分两次购买，第一次付现金购买一部分A套餐，获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱？

查看试题解析

27. 如图，二次函数 $y = a x^{2} + b x + 4$ 的图象与坐标轴分别交于A、B、C三点，其中 $A (- 3 ， 0)$ ，点 $B$ 在x轴正半轴上，连接 $A C$ 、 $B C$ .点D从点A出发，沿 $A C$ 向点C移动；同时点E从点O出发，沿x轴向点B移动，它们移动的速度都是每秒1个单位长度，当其中一点到达终点时，另一点随之停止移动，连接 $D E$ ，设移动时间为 $t s$ .

(1)、若 $t = 3$ 时， $Δ A D E$ 与 $Δ A B C$ 相似，求这个二次函数的表达式；

(2)、若 $Δ A D E$ 可以为直角三角形，求 $a$ 的取值范围.

查看试题解析
28. 已知 $Δ A B C$ 中， $∠ B A C = 90 °$ ，把中线 $A D$ 绕点D旋转至如图所示的位置，此时 $D A^{'} // A B$ ，作 $A^{'} E ⊥ B C$ ，连接 $A A^{'}$ 、 $B A^{'}$ .

(1)、若 $\sin C = \frac{3}{4}$ ，求 $Δ A^{'} D E$ 和四边形 $A^{'} D A B$ 的面积之比；

(2)、判断 $∠ B A^{'} E$ 和 $∠ D A^{'} A$ 的数量关系并说明理由.

查看试题解析